题目内容
11.给出下列四个命题:①平行于同一平面的两条直线互相平行;
②分别与两条异面直线都相交的两条直线一定是异面直线;
③若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一平面也不垂直
其中为真命题的是( )
| A. | ②和④ | B. | ②和③ | C. | ③和④ | D. | ①和② |
分析 在①中,两条直线互相平行或相交;在②中,图示法举出反例得两条直线不一定是异面直线;由面面垂直的判定定理得③正确;由面面垂直的性质定理得④正确.
解答 解:在①中,平行于同一平面的两条直线互相平行或相交,故①错误;
②分别和两条异面直线均相交的两条直线不一定是异面直线,
如右图此各情况下两直线相交,故②错误;
③若一个平面经过另一个平面的垂线,那么由面面垂直的判定定理得这两个平面相互垂直,故③正确;
④若两个平面垂直,那么由面面垂直的性质定理得一个平面内与它们的交线不垂直的直线与另一平面也不垂直,故④正确.
故选:C.
点评 本题考查命题真假的判断,是基础题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.若直线x+(1+m)y+m-2=0与直线2mx+4y+16=0没有公共点,则m的值是( )
| A. | -2 | B. | 1 | C. | 1或-2 | D. | 2或-1 |
6.某四面体的三视图如图所示,该四面体外接球的表面积为( )
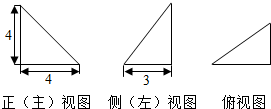

| A. | 41π | B. | $\frac{41π}{2}$ | C. | 48π | D. | 24π |
3.在梯形ABCD中,$\overrightarrow{AB}$=3$\overrightarrow{DC}$,则$\overrightarrow{BC}$等于( )
| A. | -$\frac{2}{3}$$\overrightarrow{AB}$+$\overrightarrow{AD}$ | B. | -$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{4}{3}$$\overrightarrow{AD}$ | C. | -$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AD}$ | D. | -$\frac{2}{3}$$\overrightarrow{AB}$-$\overrightarrow{AD}$ |