题目内容
19.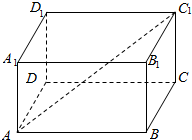 如图,在长方体ABCD-A1B1C1D1中,已知A1A=1,AD=1,AB=$\sqrt{2}$,则体对角线AC1与平面ABCD所成角的大小为30°.
如图,在长方体ABCD-A1B1C1D1中,已知A1A=1,AD=1,AB=$\sqrt{2}$,则体对角线AC1与平面ABCD所成角的大小为30°.
分析 如图所示,连接AC,可得体对角线AC1与平面ABCD所成角为∠C1AC,利用勾股定理及锐角三角函数定义求出即可.
解答 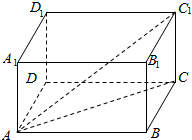 解:连接AC,可得体对角线AC1与平面ABCD所成角为∠C1AC,如图所示,
解:连接AC,可得体对角线AC1与平面ABCD所成角为∠C1AC,如图所示,
∵在长方体ABCD-A1B1C1D1中,已知A1A=1,AD=1,AB=$\sqrt{2}$,
∴C1C=A1A=1,BC=AD=1,根据勾股定理得:AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{3}$,
在Rt△C1AC中,tan∠C1AC=$\frac{C{C}_{1}}{AC}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
则∠C1AC=30°,
故答案为:30°
点评 此题考查了直线与平面所成的角,找出体对角线AC1与平面ABCD所成角为∠C1AC是解本题的关键.

练习册系列答案
相关题目
8.在△ABC中,a,b,c分别是角A,B,C的对边,a=8,b=4,A=60°,则cosB=( )
| A. | $\frac{\sqrt{13}}{4}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | -$\frac{\sqrt{3}}{4}$ | D. | -$\frac{\sqrt{13}}{4}$ |
9.向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$满足$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=0,$\overrightarrow{a}$⊥$\overrightarrow{b}$,($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{c}$,$M=\frac{|a|}{|b|}+\frac{|b|}{|c|}+\frac{|c|}{|a|}$,则M=( )
| A. | 3 | B. | $3\sqrt{2}$ | C. | $2+\frac{{\sqrt{2}}}{2}$ | D. | $1+\frac{{3\sqrt{2}}}{2}$ |




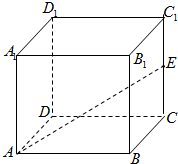 如图,已知正方体ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点,则AE与平面B1BCC1所成的角为$arctan\frac{{2\sqrt{5}}}{5}$.($arcsin\frac{2}{3}$,$arccos\frac{{\sqrt{5}}}{3}$)(结果用反三角表示)
如图,已知正方体ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点,则AE与平面B1BCC1所成的角为$arctan\frac{{2\sqrt{5}}}{5}$.($arcsin\frac{2}{3}$,$arccos\frac{{\sqrt{5}}}{3}$)(结果用反三角表示)