题目内容
P为正方体ABCD-A1B1C1D1对角线BD1上的一点,且BP=λBD1(λ∈(0,1).下面结论:
①AD1⊥C1P;
②若BD1⊥平面PAC,则λ=
;
③若△PAC为钝角三角形,则λ∈(0,
);
④若λ∈(
,1),则△PAC为锐角三角形.
其中正确的结论为 .(写出所有正确结论的序号)
①AD1⊥C1P;
②若BD1⊥平面PAC,则λ=
| 1 |
| 3 |
③若△PAC为钝角三角形,则λ∈(0,
| 1 |
| 2 |
④若λ∈(
| 2 |
| 3 |
其中正确的结论为
考点:用空间向量求直线间的夹角、距离,棱柱的结构特征
专题:空间位置关系与距离,空间角
分析:画出图形,直接判断①AD1⊥C1P的正误;
利用正方体的特征,判断②若BD1⊥平面PAC,则λ=
,的正误;
通过λ=
,判断△PAC是否为钝角三角形,判断λ∈(0,
)的正误;
通过建立空间直角坐标系,判断④若λ∈(
,1),则△PAC为锐角三角形,判断④的正误.
利用正方体的特征,判断②若BD1⊥平面PAC,则λ=
| 1 |
| 3 |
通过λ=
| 1 |
| 2 |
| 1 |
| 2 |
通过建立空间直角坐标系,判断④若λ∈(
| 2 |
| 3 |
解答:
 解:如图①中,AD1与C1P是共面直线,是相交直线,∴①不正确;
解:如图①中,AD1与C1P是共面直线,是相交直线,∴①不正确;
对于②若BD1⊥平面PAC,几何体是正方体,∴P在平面AB1C中,则λ=
;②正确;
对于③,当P为BD1的中点时,若△PAC为钝角三角形,PA=PC=
a,AC=
a,此时∠APC=120°,∴则λ∈(0,
)不正确;
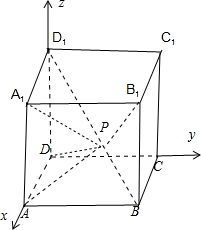
对于④,建立如图所示的空间直角坐标系,不妨设正方体的棱长|AB|=3,
则A(3,0,0),B(3,3,0),C(0,3,0),D(0,0,0),A1(3,0,3),B1(3,3,3),C1(0,3,3),D1(0,0,3),
∴
=(-3,-3,3),设P(x,y,z),∵
=
=(-2,-2,2),∴
=
+(-2,-2,2)=(1,1,2).
=
+
=(-2,1,2),
=(1,-2,2)∴cos∠APC=
=0,∠APC=90°.
若λ∈(
,1),则△PAC为锐角三角形.正确,
故答案为:②④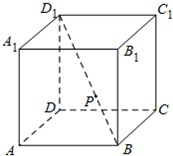
 解:如图①中,AD1与C1P是共面直线,是相交直线,∴①不正确;
解:如图①中,AD1与C1P是共面直线,是相交直线,∴①不正确;对于②若BD1⊥平面PAC,几何体是正方体,∴P在平面AB1C中,则λ=
| 1 |
| 3 |
对于③,当P为BD1的中点时,若△PAC为钝角三角形,PA=PC=
| ||
| 2 |
| 2 |
| 1 |
| 2 |
对于④,建立如图所示的空间直角坐标系,不妨设正方体的棱长|AB|=3,
则A(3,0,0),B(3,3,0),C(0,3,0),D(0,0,0),A1(3,0,3),B1(3,3,3),C1(0,3,3),D1(0,0,3),
∴
| BD1 |
| BP |
|
| DP |
| DB |
| AP |
| AD |
| DP |
| CP |
| ||||
|
|
若λ∈(
| 2 |
| 3 |
故答案为:②④

点评:本题考查空间直角坐标系的应用,夹角与距离的关系,考查空间想象能力以及计算能力.

练习册系列答案
相关题目


