题目内容
已知tanx=-2,求
的值.
| sin2x-3sinxcosx-cos2x |
考点:同角三角函数基本关系的运用
专题:计算题,三角函数的求值
分析:sin2x-3sinxcosx-cos2x=
=
,再代入,即可得出结论.
| sin2x-3sinxcosx-cos2x |
| sin2x+cos2x |
| tan2x-3tanx-1 |
| tan2x+1 |
解答:
解:∵tanx=-2,
∴sin2x-3sinxcosx-cos2x=
=
=
=
,
∴
=
.
∴sin2x-3sinxcosx-cos2x=
| sin2x-3sinxcosx-cos2x |
| sin2x+cos2x |
| tan2x-3tanx-1 |
| tan2x+1 |
| 4+6-1 |
| 4+1 |
| 9 |
| 5 |
∴
| sin2x-3sinxcosx-cos2x |
3
| ||
| 5 |
点评:本题考查同角三角函数关系,考查学生的计算能力,正确弦化切是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
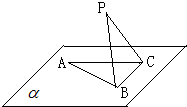 如图,△ABC在平面α内,∠ACB=90°,AB=2BC=2,P为平面α外一个动点,且PC=
如图,△ABC在平面α内,∠ACB=90°,AB=2BC=2,P为平面α外一个动点,且PC=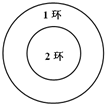 如图,一半径为
如图,一半径为 如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=
如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=