题目内容
如图1,椭圆E:
+
=1(a>b>0)的左、右焦点分别为F1F2,左、右顶点分别为A1,A2,T(1,
)为椭圆上一点,且TF2垂直于x轴.

(Ⅰ)求椭圆E的方程;
(Ⅱ)给出命题:“已知P是椭圆E上异于A1,A2的一点,直线 A1P,A2P分别交直线l:x=t(t为常数)于不同两点M,N,点Q在直线l上.若直线PQ与椭圆E有且只有一个公共点P,则Q为线段MN的中点”,写出此命题的逆命题,判断你所写出的命题的真假,并加以证明;
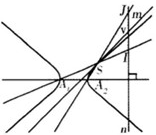
(Ⅲ)试研究(Ⅱ)的结论,根据你的研究心得,在图2中作出与该双曲线有且只有一个公共点S的直线m,并写出作图步骤.注意:所作的直线不能与双曲线的渐近线平行.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |

(Ⅰ)求椭圆E的方程;
(Ⅱ)给出命题:“已知P是椭圆E上异于A1,A2的一点,直线 A1P,A2P分别交直线l:x=t(t为常数)于不同两点M,N,点Q在直线l上.若直线PQ与椭圆E有且只有一个公共点P,则Q为线段MN的中点”,写出此命题的逆命题,判断你所写出的命题的真假,并加以证明;
(Ⅲ)试研究(Ⅱ)的结论,根据你的研究心得,在图2中作出与该双曲线有且只有一个公共点S的直线m,并写出作图步骤.注意:所作的直线不能与双曲线的渐近线平行.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据T(1,
)为椭圆上一点,且TF2垂直于x轴,求出c,利用椭圆的定义,求出a,即可求椭圆E的方程;
(Ⅱ)逆命题为真命题.设P(x0,y0)(x0≠±2),求出A1P,A2P的方程,可得M,N的坐标,进而可得Q的坐标,求出PQ的方程,代入椭圆方程,求出△=0,即可得出结论;
(Ⅲ)利用(Ⅱ),可得结论.
| 3 |
| 2 |
(Ⅱ)逆命题为真命题.设P(x0,y0)(x0≠±2),求出A1P,A2P的方程,可得M,N的坐标,进而可得Q的坐标,求出PQ的方程,代入椭圆方程,求出△=0,即可得出结论;
(Ⅲ)利用(Ⅱ),可得结论.
解答:
 解:(Ⅰ)∵T(1,
解:(Ⅰ)∵T(1,
)为椭圆上一点,且TF2垂直于x轴,
∴c=1,
在Rt△TF1F2,|TF2|=
,|F1F2|=2,∴|TF1|=
,
∴2a=|TF1|+|TF2|=4,
∴a=2,
∴b=
=
∴椭圆E的方程为
+
=1;
(Ⅱ)逆命题:“已知P是椭圆E上异于A1,A2的一点,直线 A1P,A2P分别交直线l:x=t(t为常数)于不同两点M,N,点Q在直线l上.若Q为线段MN的中点,则直线PQ与椭圆E有且只有一个公共点P”,为真命题.
证明如下:设P(x0,y0)(x0≠±2),则
+
=1,
lA1P:y=
(x+2);lA2P:y=
(x-2),
∴M(t,
),N(t,
),
设MN的中点为Q(x1,y1),则x1=t,y1=
,
∵x02-4=
,
∴y1=
=
,
∴Q(t,
),
∴kPQ=
=
,
∴PQ的方程为y=
(x-x0)+y0,即y=
x+
代入椭圆方程,消去y可得
x2-
x+
-1=0,
∴△=(
)2-4•
•(
-1)=
=0,
∴直线PQ与椭圆E有且只有一个公共点P;
(Ⅲ)如图,①任作一条不过点S的直线n垂直于双曲线的实轴;②作直线A1S,A2S分别交直线n于I,J两点;③作线段IJ的中点V,连接SV,则直线SV即为所求的直线m.
 解:(Ⅰ)∵T(1,
解:(Ⅰ)∵T(1,| 3 |
| 2 |
∴c=1,
在Rt△TF1F2,|TF2|=
| 3 |
| 2 |
| 5 |
| 2 |
∴2a=|TF1|+|TF2|=4,
∴a=2,
∴b=
| a2-c2 |
| 3 |
∴椭圆E的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)逆命题:“已知P是椭圆E上异于A1,A2的一点,直线 A1P,A2P分别交直线l:x=t(t为常数)于不同两点M,N,点Q在直线l上.若Q为线段MN的中点,则直线PQ与椭圆E有且只有一个公共点P”,为真命题.
证明如下:设P(x0,y0)(x0≠±2),则
| x02 |
| 4 |
| y02 |
| 3 |
lA1P:y=
| y0 |
| x0+2 |
| y0 |
| x0-2 |
∴M(t,
| y0(t+2) |
| x0+2 |
| y0(t-2) |
| x0-2 |
设MN的中点为Q(x1,y1),则x1=t,y1=
| y0(x0t-4) |
| x02-4 |
∵x02-4=
| -4y02 |
| 3 |
∴y1=
| y0(x0t-4) |
| x02-4 |
| -3(x0t-4) |
| 4y0 |
∴Q(t,
| -3(x0t-4) |
| 4y0 |
∴kPQ=
| ||
| t-x0 |
| -3x0 |
| 4y0 |
∴PQ的方程为y=
| -3x0 |
| 4y0 |
| -3x0 |
| 4y0 |
| 3 |
| y0 |
代入椭圆方程,消去y可得
| 3 |
| 4y02 |
| 3x0 |
| 2y02 |
| 3 |
| y02 |
∴△=(
| 3x0 |
| 2y02 |
| 3 |
| 4y02 |
| 3 |
| y02 |
| 9x02+12y02-36 |
| 4y04 |
∴直线PQ与椭圆E有且只有一个公共点P;
(Ⅲ)如图,①任作一条不过点S的直线n垂直于双曲线的实轴;②作直线A1S,A2S分别交直线n于I,J两点;③作线段IJ的中点V,连接SV,则直线SV即为所求的直线m.
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
某程序框图如图所示,若该程序运行后输出的结果不大于37,则输入的整数i的最大值为( )


| A、3 | B、4 | C、5 | D、6 |
如图所示图形中是四棱锥三视图的是( )
A、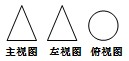 |
B、 |
C、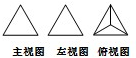 |
D、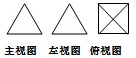 |