题目内容
解方程及不等式
(1)2x2-x-3=0 (2)x2+4x-5≤0
(3)|x-3|>10 (4)x2-6x+8>0.
(1)2x2-x-3=0 (2)x2+4x-5≤0
(3)|x-3|>10 (4)x2-6x+8>0.
考点:一元二次不等式的解法
专题:函数的性质及应用
分析:(1)通过因式分解,可得出.
(2)通过因式分解,利用一元二次不等式的解法即可得出.
(3)根据绝对值的意义解答即可,
(4)通过因式分解,利用一元二次不等式的解法即可得出.
(2)通过因式分解,利用一元二次不等式的解法即可得出.
(3)根据绝对值的意义解答即可,
(4)通过因式分解,利用一元二次不等式的解法即可得出.
解答:
解:(1)∵2x2-x-3=0
∴(x+)(2x-3)=0,
∴x=-1或x=
,
∴原方程的解是x=-1或x=
;
(2)∵x2+4x-5≤0
∴(x-1)(x+5)≤0,
∴-5≤x≤1,
∴原不等式的解集是:[-5,1];
(3)∵|x-3|>10,
∴x-3<-10,或x-3>10
解得x<-7或x>13,
∴原不等式的解集是(-∞,-7)∪(13,+∞);
(4)∵x2-6x+8>0,
∴(x-2)(x-4)>0,
∴x<2或x>4,
∴原不等式的解集是(-∞,2∪(4,∞);
∴(x+)(2x-3)=0,
∴x=-1或x=
| 3 |
| 2 |
∴原方程的解是x=-1或x=
| 3 |
| 2 |
(2)∵x2+4x-5≤0
∴(x-1)(x+5)≤0,
∴-5≤x≤1,
∴原不等式的解集是:[-5,1];
(3)∵|x-3|>10,
∴x-3<-10,或x-3>10
解得x<-7或x>13,
∴原不等式的解集是(-∞,-7)∪(13,+∞);
(4)∵x2-6x+8>0,
∴(x-2)(x-4)>0,
∴x<2或x>4,
∴原不等式的解集是(-∞,2∪(4,∞);
点评:本题考查了一元二次不等式的解法,绝对值不等式的解法,属于基础题.

练习册系列答案
相关题目
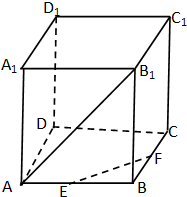
在正方体EF⊥A1D中,A1D∥B1C分别为AB、BC中点,则异面直线EF与AB1所成角的余弦值为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知x,y满足
记目标函数z=2x+y的最小值为1,最大值为7,则b,c的值分别为( )
|
| A、-1,-2 | B、-2,-1 |
| C、1,2 | D、1,-2 |