题目内容
现有语文、数学、英语、物理和化学共5本书，从中任取1本，取出的是理科书的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：古典概型及其概率计算公式
专题：概率与统计
分析：根据随机事件概率大小的求法，要弄清楚两点：①符合条件的情况数目；②全部情况的总数；二者的比值就是其发生的概率的大小．用理科书的本数除以书的总本数5即为所求的概率．
解答：
解：5本书中一共有3本理科书：数学、物理、化学，
所以取出的是理科书的概率为：
．
故选：C．
所以取出的是理科书的概率为：
| 3 |
| 5 |
故选：C．
点评：解答此题的关键是要弄清楚：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=
．
| m |
| n |
练习册系列答案
相关题目
已知某四棱锥，底面是边长为2的正方形，且俯视图如图所示．若该四棱锥的侧视图为直角三角形，则它的体积为函数f（x）=（
）x-4的零点为（ ）
| 1 |
| 2 |
| A、-2 | B、-1 | C、0 | D、2 |
使不等式sinx≥
（x∈R）成立的x的集合是（ ）
| ||
| 2 |
A、{x|x≥
| ||||
B、{x|2kπ+
| ||||
C、{x|
| ||||
D、{x|x≥2kπ+
|
在正方体ABCD-A1B1C1D1中，AC与A1D的夹角为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
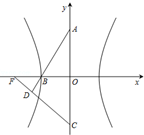如图，双曲线的中心在坐标原点O，A，C分别是双曲线虚轴的上、下顶点，B是双曲线的左顶点，F为双曲线的左焦点，直线AB与FC相交于点D．若双曲线的离心率为3，则∠BDF的余弦值是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若f（x）是定义在R上的可导函数，且满足（x-1）f′（x）≥0，则必有（ ）
| A、f（0）+f（2）＜2f（1） |
| B、f（0）+f（2）＞2f（1） |
| C、f（0）+f（2）≤2f（1） |
| D、f（0）+f（2）≥2f（1） |
已知双曲线C：
-
=1（a＞0，b＞0）的焦距为2
，若抛物线x2=16y的焦点到双曲线C的渐近线的距离为
，则双曲线C的方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
8
| ||
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、x2-
|
下列有关命题的说法正确的是（ ）
A、若向量
| ||||||||||||
B、“α=30”是“sinα=
| ||||||||||||
| C、命题“?x∈R，使得x2+x-1＜0”的否定是：“?x∈R，均有x2+x-1＞0” | ||||||||||||
| D、命题“若x=y，则sinx=siny”的逆否命题为真命题 |