题目内容
已知离心率为
的椭圆T:
+
=1(a>0,b>0)过点M(0,1),过点M引两条互相垂直的直线l1,l2,若P为椭圆上任意一点,记点P到两直线的距离分别为d1,d2,则d12+d22的最大值是( )
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、5 | ||
C、
| ||
| D、2 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意可知圆的半径等于1,椭圆的短半轴等于1,根据离心率为
,结合a2=b2+c2求出椭圆的长半轴,则椭圆方程可求.因为两直线l1、l2相互垂直,所以点P到两直线的距离d1、d2的平方和可转化为P点到M点距离的平方,利用点P在椭圆上把要求的式子化为含P点纵坐标的函数,利用二次函数可求最大值.
| ||
| 2 |
解答:
解:椭圆T:
+
=1(a>0,b>0)过点M(0,1),∴b=1,
∵离心率为
,∴a=2,c=
,
∴椭圆方程为
+y2=1,
设P(x0,y0),则
∵l1⊥l2,则d12+d22=PM2=x02+(y0-1)2,
∵
+y02=1,
∴d12+d22=-3(y0+
)2+
,
∵-1≤y0≤1,∴当y0=-
时,d12+d22取得最大值为
.
故选:A.
| x2 |
| a2 |
| y2 |
| b2 |
∵离心率为
| ||
| 2 |
| 3 |
∴椭圆方程为
| x2 |
| 4 |
设P(x0,y0),则
∵l1⊥l2,则d12+d22=PM2=x02+(y0-1)2,
∵
| x02 |
| 4 |
∴d12+d22=-3(y0+
| 1 |
| 3 |
| 16 |
| 3 |
∵-1≤y0≤1,∴当y0=-
| 1 |
| 3 |
| 16 |
| 3 |
故选:A.
点评:本题考查了椭圆的标准方程,直线和圆锥曲线的位置关系,考查了数学转化思想和方程思想方法,训练了学生的计算能力,属中档题.

练习册系列答案
相关题目
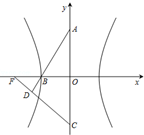 如图,双曲线的中心在坐标原点O,A,C分别是双曲线虚轴的上、下顶点,B是双曲线的左顶点,F为双曲线的左焦点,直线AB与FC相交于点D.若双曲线的离心率为3,则∠BDF的余弦值是( )
如图,双曲线的中心在坐标原点O,A,C分别是双曲线虚轴的上、下顶点,B是双曲线的左顶点,F为双曲线的左焦点,直线AB与FC相交于点D.若双曲线的离心率为3,则∠BDF的余弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若a>0,b>0,则p=
+
与q=a+b的大小关系为( )
| b2 |
| a |
| a2 |
| b |
| A、p>q | B、p≥q |
| C、p<q | D、p≤q |
抛物线x=
y2的准线过双曲线
-
=1的右焦点,则m的值是( )
| 1 |
| m |
| x2 |
| 12 |
| y2 |
| 4 |
| A、-8 | B、-16 | C、4 | D、16 |
下列有关命题的说法正确的是( )
A、若向量
| ||||||||||||
B、“α=30”是“sinα=
| ||||||||||||
| C、命题“?x∈R,使得x2+x-1<0”的否定是:“?x∈R,均有x2+x-1>0” | ||||||||||||
| D、命题“若x=y,则sinx=siny”的逆否命题为真命题 |
已知数列{an}中,a3=2,a7=1,若{
}为等差数列,则a19=( )
| 1 |
| an+1 |
| A、0 | ||
B、
| ||
C、
| ||
| D、2 |