题目内容
正项等比数列{an}的前n项和为Sn,a4=16,且a2,a3的等差中项为S2.
(1)求数列{an}的通项公式;
(2)设bn=
,数列{bn}的前n项和为Tn,求证:Tn<
.
(1)求数列{an}的通项公式;
(2)设bn=
| n |
| a2n-1 |
| 8 |
| 9 |
考点:数列与不等式的综合,等比数列的通项公式
专题:等差数列与等比数列
分析:(1)由已知条件得
,由此能求出an=2n.
(2)bn=
=
,由此利用错位相减求和法求出Tn=
-
,从而能证明Tn<
|
(2)bn=
| n |
| a2n-1 |
| n |
| 22n-1 |
| 8 |
| 9 |
| 16+12n |
| 9•22n+1 |
| 8 |
| 9 |
解答:
(1)解:设等比数列{an}的公比为q,(q>0),
∵a4=16,且a2,a3的等差中项为S2,
∴
,
解得
,∴an=2n.
(2)证明:bn=
=
,
Tn=
+
+
+
+…+
,①
∴
Tn=
+
+
+…+
+
,②
①-②,得
Tn=
+
+
+
+
-
=
-
=
-
,
∴Tn=
-
.∵n∈N*,
>0,∴x>1.
∵n∈N*,
>0,
∴Tn<
.
∵a4=16,且a2,a3的等差中项为S2,
∴
|
解得
|
(2)证明:bn=
| n |
| a2n-1 |
| n |
| 22n-1 |
Tn=
| 1 |
| 2 |
| 2 |
| 23 |
| 3 |
| 25 |
| 4 |
| 27 |
| n |
| 22n-1 |
∴
| 1 |
| 4 |
| 1 |
| 23 |
| 2 |
| 25 |
| 3 |
| 27 |
| 2n-1 |
| 22n-1 |
| n |
| 22n+1 |
①-②,得
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 23 |
| 1 |
| 25 |
| 1 |
| 27 |
| 1 |
| 22n-1 |
| n |
| 22n+1 |
=
| ||||
1-
|
| n |
| 22n+1 |
| 2 |
| 3 |
| 4+3n |
| 3•22n+1 |
∴Tn=
| 8 |
| 9 |
| 16+12n |
| 9•22n+1 |
| 16+12n |
| 9•22n+1 |
∵n∈N*,
| 16+12n |
| 9•22n+1 |
∴Tn<
| 8 |
| 9 |
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意错位相减求和法的合理运用.

练习册系列答案
相关题目
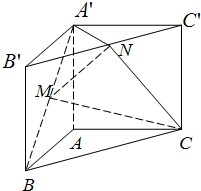 如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=
如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=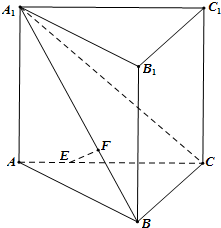 如图,在直三棱柱ABC-A1B1C1(侧棱和底面垂直的棱柱)中,平面A1BC⊥侧面A1ABB1,AB=BC=AA1=3,线段AC、A1B上分别有一点E、F且满足2AE=EC,2BF=FA1.
如图,在直三棱柱ABC-A1B1C1(侧棱和底面垂直的棱柱)中,平面A1BC⊥侧面A1ABB1,AB=BC=AA1=3,线段AC、A1B上分别有一点E、F且满足2AE=EC,2BF=FA1.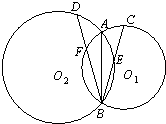 如图,假设两圆O1和O2交于A、B,⊙O1的弦BC交⊙O2于E,⊙O2的弦BD交⊙O1于F,证明:
如图,假设两圆O1和O2交于A、B,⊙O1的弦BC交⊙O2于E,⊙O2的弦BD交⊙O1于F,证明: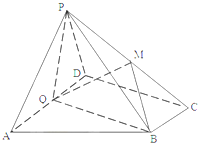 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD中点,M是棱PC上的点,PD=PA=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD中点,M是棱PC上的点,PD=PA=2,BC=