题目内容
数列{an}前n项和Sn=n2+2n-2,对数列{an}的描述正确的是( )
| A、数列{an}为递增数列 |
| B、数列{an}为递减数列 |
| C、数列{an}为等差数列 |
| D、数列{an}为等比数列 |
考点:等比关系的确定,数列的函数特性
专题:等差数列与等比数列
分析:利用Sn=n2+2n-2⇒an=
,利用函数的单调性及等差数列与等比数列的概念对A、B、C、D四个选项逐一分析即可得到答案.
|
解答:
解:Sn=n2+2n-2⇒an=
,
对于A:a1<a2<…<an,
所以是递增数列,不是递减数列,可排除B;
对于C:a1=1,a2=5,a3=7,a3-a2≠a2-a1,数列{an}不是等差数列,可排除C;
对于D:
≠
,即数列{an}也不是等比数列,可排除D.
故选A.
|
对于A:a1<a2<…<an,
所以是递增数列,不是递减数列,可排除B;
对于C:a1=1,a2=5,a3=7,a3-a2≠a2-a1,数列{an}不是等差数列,可排除C;
对于D:
| a2 |
| a1 |
| a3 |
| a2 |
故选A.
点评:本题考查等比关系与等差关系的确定,考查数列递推关系的应用及数列的单调性,属于中档题.

练习册系列答案
相关题目
若满足条件C=30°、AB=
、BC=a的△ABC有两个,那么a的取值范围是( )
| 6 |
A、(1,
| ||||
B、(
| ||||
C、(
| ||||
D、(1,2
|
若角α的终边在直线y=2x上,则
的值为( )
| 2sinα-cosα |
| sinα+2cosα |
| A、0 | ||
B、
| ||
| C、1 | ||
D、
|
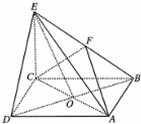 在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.