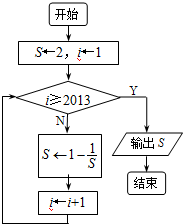
题目内容
若角α的终边在直线y=2x上，则
的值为（ ）
| 2sinα-cosα |
| sinα+2cosα |
| A、0 | ||
B、
| ||
| C、1 | ||
D、
|
考点：同角三角函数基本关系的运用,三角函数线
专题：三角函数的求值
分析：依题意，tanα=2，将所求的关系式中的“弦”化“切”即可求得答案．
解答：
解：∵角α的终边在直线y=2x上，
∴tanα=2，
∴
=
=
，
故选：B．
∴tanα=2，
∴
| 2sinα-cosα |
| sinα+2cosα |
| 2tanα-1 |
| tanα+2 |
| 3 |
| 4 |
故选：B．
点评：本题考查同角三角函数基本关系的运用，“弦”化“切”是关键，属于基础题．
练习册系列答案
相关题目
数列{an}前n项和Sn=n2+2n-2，对数列{an}的描述正确的是（ ）
| A、数列{an}为递增数列 |
| B、数列{an}为递减数列 |
| C、数列{an}为等差数列 |
| D、数列{an}为等比数列 |
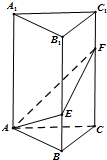如图，在直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=2，AA1=6，点E、F分别在棱BB1、CC1上，且BE=