题目内容
已知点P(x,y)在曲线x2-y2=1上运动,则
-
的取值范围是 .
| 2y |
| x |
| 1 |
| x2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:点P(x,y)在曲线x2-y2=1上运动,设x=secθ,y=tanθ,θ∈[0,2π)(θ≠
,
).则
-
=(sinθ+1)2-2,利用正弦函数与二次函数的单调性即可得出.
| π |
| 2 |
| 3π |
| 2 |
| 2y |
| x |
| 1 |
| x2 |
解答:
解:点P(x,y)在曲线x2-y2=1上运动,设x=secθ,y=tanθ,θ∈[0,2π)(θ≠
,
).
则
-
=
-
=2sinθ-cos2θ=(sinθ+1)2-2,
∵-1<sinθ<1,∴(sinθ+1)2-2∈(-2,2),
∴
-
的取值范围是(-2,2).
故答案为:(-2,2).
| π |
| 2 |
| 3π |
| 2 |
则
| 2y |
| x |
| 1 |
| x2 |
| 2tanθ |
| secθ |
| 1 |
| sec2θ |
∵-1<sinθ<1,∴(sinθ+1)2-2∈(-2,2),
∴
| 2y |
| x |
| 1 |
| x2 |
故答案为:(-2,2).
点评:本题考查了双曲线的参数方程、正弦函数与二次函数的单调性,考查了计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
数列{an}前n项和Sn=n2+2n-2,对数列{an}的描述正确的是( )
| A、数列{an}为递增数列 |
| B、数列{an}为递减数列 |
| C、数列{an}为等差数列 |
| D、数列{an}为等比数列 |
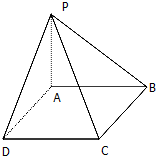 如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=
如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=