题目内容
已知函数f(x)=lg
(a∈R).
(1)试确定f(x)的定义域;
(2)如果函数F(x)=2f(x)-f(2x)有两个不同的零点,求a的取值范围.
| 1+2xa |
| 2 |
(1)试确定f(x)的定义域;
(2)如果函数F(x)=2f(x)-f(2x)有两个不同的零点,求a的取值范围.
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:(1)由 函数f(x)的解析式可得 1+2x•a>0,分当a≥0时,和当a<0时两种情况,分别求得f(x)的定义域.
(2)由题意可得2f(x)=f(2x)有两个不同的实数根,即(a2-2a)22x+2a•2x-1=0 有两个不同的实数根,及方程(a2-2a)t2+2a•t-1=0 关于变量t有两个不同的正实数根,由△>0,且两根之和大于0,两根之积大于0,求得a的范围.
(2)由题意可得2f(x)=f(2x)有两个不同的实数根,即(a2-2a)22x+2a•2x-1=0 有两个不同的实数根,及方程(a2-2a)t2+2a•t-1=0 关于变量t有两个不同的正实数根,由△>0,且两根之和大于0,两根之积大于0,求得a的范围.
解答:
解:(1)∵函数f(x)=lg
(a∈R),∴1+2x•a>0,
∴当a≥0时,1+2x•a>0 恒成立,f(x)的定义域为R;
当a<0时,由2x>-
,求得 x>log2(-
),f(x)的定义域为(log2(-
),+∞).
(2)由题意可得2f(x)=f(2x)有两个不同的实数根,即lg (
)2=lg
有两个不同的实数根,
即 (
)2=
有两个不同的实数根,即(a2-2a)22x+2a•2x-1=0 有两个不同的实数根,
令t=2x>0,则有(a2-2a)t2+2a•t-1=0 关于变量t有两个不同的实数根,
∴△=8a(a-1)>0,且两根之和
>0,两根之积
>0,求得1<a<2,
综上可得,a的范围为{a|1<a<2}.
| 1+2xa |
| 2 |
∴当a≥0时,1+2x•a>0 恒成立,f(x)的定义域为R;
当a<0时,由2x>-
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
(2)由题意可得2f(x)=f(2x)有两个不同的实数根,即lg (
| 1+a•2x |
| 2 |
| 1+2•22x |
| 2 |
即 (
| 1+a•2x |
| 2 |
| 1+2•22x |
| 2 |
令t=2x>0,则有(a2-2a)t2+2a•t-1=0 关于变量t有两个不同的实数根,
∴△=8a(a-1)>0,且两根之和
| 2a |
| 2a-a2 |
| -1 |
| a2-2a |
综上可得,a的范围为{a|1<a<2}.
点评:本题主要考查对数函数的定义域,方程根的存在性及个数判断,体现了分类讨论、转化的数学思想,属于基础题.

练习册系列答案
相关题目
数列{an}前n项和Sn=n2+2n-2,对数列{an}的描述正确的是( )
| A、数列{an}为递增数列 |
| B、数列{an}为递减数列 |
| C、数列{an}为等差数列 |
| D、数列{an}为等比数列 |
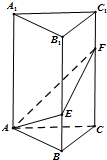 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE=
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE=