题目内容
8.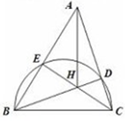 如图,以锐角△ABC的边BC为直径的半圆分别与AC、AB交于点D、E,BD、CE的交点为H,且BC=2.
如图,以锐角△ABC的边BC为直径的半圆分别与AC、AB交于点D、E,BD、CE的交点为H,且BC=2.(Ⅰ)证明:AB•CD=BD•HC;
(Ⅱ)求BE•BA+CD•CA的值.
分析 (Ⅰ)证明△BAD∽△CHD,即可证明AB•CD=BD•HC;
(Ⅱ)延长AH交BC于F,AF⊥BC,A,E,F,C四点共圆,A,B,F,D四点共圆,由割线定理得BE•BA=BF•BC,CD•CA=CF•CB,即可求BE•BA+CD•CA的值.
解答 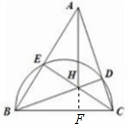 (Ⅰ)证明:因为以BC为直径的半圆分别与AC,AB交于点D,E
(Ⅰ)证明:因为以BC为直径的半圆分别与AC,AB交于点D,E
所以∠BDC=∠ADB=90°,
所以 A,E,H,D四点共圆
所以∠BAD=∠CHD
所以△BAD∽△CHD(AA)
所以$\frac{AB}{HC}=\frac{BD}{CD}$,所以AB•CD=BD•HC;
(Ⅱ)解:∵BC是直径,∴BD⊥AC,CE⊥AB,
∴H为△ABC的垂心,
故延长AH交BC于F,AF⊥BC,
∴A,E,F,C四点共圆,A,B,F,D四点共圆,
由割线定理得BE•BA=BF•BC,CD•CA=CF•CB,
两式相加可得BE•BA+CD•CA=BF•BC+CF•CB=BC2=4
∴所求代数式的值是4.
点评 本题考查三角形相似的判定与性质,考查四点共圆,考查割线定理的运用,属于中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
18.下表是某校高三一次月考5个班级的数学、物理的平均成绩:
(Ⅰ)一般来说,学生的物理成绩与数学成绩具有线性相关关系,根据上表提供的数据,求两个变量x,y的线性回归方程$\hat y=\hat bx+\hat a$;
(Ⅱ)从以上5个班级中任选两个参加某项活动,求至少有一个班级数学平均分在115分以上的概率.
附:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.
| 班级 | 1 | 2 | 3 | 4 | 5 |
| 数学(x分) | 111 | 113 | 119 | 125 | 127 |
| 物理(y分) | 92 | 93 | 96 | 99 | 100 |
(Ⅱ)从以上5个班级中任选两个参加某项活动,求至少有一个班级数学平均分在115分以上的概率.
附:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.
13.执行如图所示的程序框图,则输出的k=( )
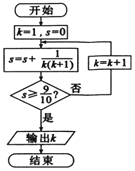

| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
20.执行如图所示的程序框图,输出s的值为( )
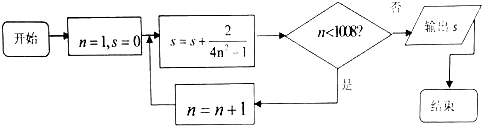

| A. | 1 | B. | $\frac{2018}{2019}$ | C. | $\frac{2018}{2017}$ | D. | $\frac{2016}{2017}$ |
17.已知圆M过定点(0,1)且圆心M在抛物线y=$\frac{1}{2}$x2上运动,若x轴截圆M所得的弦为|PQ|,则弦长|PQ|等于( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | 4 |
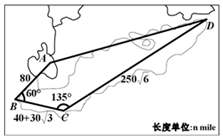 某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,$BC=40+30\sqrt{3}$nmile,$CD=250\sqrt{6}$nmile.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,则收到指令时该轮船到城市C的距离是100nmile.
某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,$BC=40+30\sqrt{3}$nmile,$CD=250\sqrt{6}$nmile.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,则收到指令时该轮船到城市C的距离是100nmile.