题目内容
13.执行如图所示的程序框图,则输出的k=( )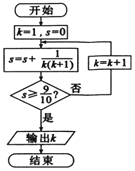
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
分析 由程序框图结合数列的裂项法进行求解即可.
解答 解:∵$\frac{1}{k(k+1)}$=$\frac{1}{k}$-$\frac{1}{k+1}$,
∴s=$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{k(k+1)}$=1$-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+$…+$\frac{1}{k}$-$\frac{1}{k+1}$=1-$\frac{1}{k+1}$,
由S≥$\frac{9}{10}$得1-$\frac{1}{k+1}$≥$\frac{9}{10}$得$\frac{1}{k+1}$≤$\frac{1}{10}$,即k+1≥10,则k≥9,
故选:C
点评 本题主要考查程序框图的应用,根据数列求和以及裂项法是解决本题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
3.设集合A={x|x2-3x+2≤0},B={(x,y)|x∈A,y∈A},则A∩B=( )
| A. | A | B. | B | C. | A∪B | D. | ∅ |
1.某工厂生产一种螺栓,在正常情况下,螺栓的直径X(单位:mm)服从正态分布X~N(100,1).现加工10个螺栓的尺寸(单位:mm)如下:
101.7,100.3,99.6,102.4,98.2,103.2,101.1,98.8,100.4,100.0.
X~N(μ,σ2)有P(μ-2σ<X<μ+2σ)=0.954,P(μ-3σ<X<μ+3σ)=0.997.根据行业标准,概率低于0.003视为小概率事件,工人随机将其中的8个交与质检员检验,则质检员认为设备需检修的概率为( )
101.7,100.3,99.6,102.4,98.2,103.2,101.1,98.8,100.4,100.0.
X~N(μ,σ2)有P(μ-2σ<X<μ+2σ)=0.954,P(μ-3σ<X<μ+3σ)=0.997.根据行业标准,概率低于0.003视为小概率事件,工人随机将其中的8个交与质检员检验,则质检员认为设备需检修的概率为( )
| A. | $\frac{44}{45}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{41}{45}$ |
18.集合M={(x,y)|x+y≤1,y≤x,y≥-1},N={(x,y)|(x-2)2+y2=r2,r>0},若M∩N≠∅,则r的取值范围为( )
| A. | $[{\frac{{\sqrt{2}}}{2},3}]$ | B. | $[{1,\sqrt{10}}]$ | C. | $[{\frac{{\sqrt{2}}}{2},\sqrt{10}}]$ | D. | $[{1,\frac{{\sqrt{10}}}{2}}]$ |
2.已知复数z=3+4i,则|z|等于( )
| A. | 25 | B. | 12 | C. | 7 | D. | 5 |
3.己知α为第二象限角,cosa=-$\frac{3}{5}$,则sin2α=( )
| A. | -$\frac{24}{25}$ | B. | -$\frac{12}{25}$ | C. | $\frac{12}{25}$ | D. | $\frac{24}{25}$ |
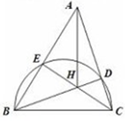 如图,以锐角△ABC的边BC为直径的半圆分别与AC、AB交于点D、E,BD、CE的交点为H,且BC=2.
如图,以锐角△ABC的边BC为直径的半圆分别与AC、AB交于点D、E,BD、CE的交点为H,且BC=2.