题目内容
16.设f(x)=|x+a|-|x+1|.(Ⅰ)求不等式f(a)>1的解集;
(Ⅱ)当x∈R时,f(x)≤2a(a∈R),求实数a的取值范围.
分析 (Ⅰ)f(a)>1,即|2a|-|a+1|>1,分类讨论,即可求不等式f(a)>1的解集;
(Ⅱ)f(x)=|x+a|-|x+1|≤|(x+a)-(x-1)|=|a-1|.令|a-1|≤2a,即可求实数a的取值范围.
解答 解:(Ⅰ)f(a)>1,即|2a|-|a+1|>1,
a≤-1,不等式化为-2a+a+1>1,即a<0,∴a≤-1;
-1<a≤0,不等式化为-2a-(a+1)>1,即a<-$\frac{2}{3}$,∴-1<a<-$\frac{2}{3}$;
a>0,不等式化为2a-(a+1)>1,即a>2,∴a>2,
故不等式的解集为{a|a<-$\frac{2}{3}$或a>2};
(Ⅱ)f(x)=|x+a|-|x+1|≤|(x+a)-(x-1)|=|a-1|.
令|a-1|≤2a,
显然a>0,两边平方得a2-2a+1≤4a2,即3a2+2a-1≥0,
∴a≥$\frac{1}{3}$.
点评 本题考查不等式的解法,考查恒成立问题,考查绝对值不等式的运用,属于中档题.

练习册系列答案
相关题目
1.某工厂生产一种螺栓,在正常情况下,螺栓的直径X(单位:mm)服从正态分布X~N(100,1).现加工10个螺栓的尺寸(单位:mm)如下:
101.7,100.3,99.6,102.4,98.2,103.2,101.1,98.8,100.4,100.0.
X~N(μ,σ2)有P(μ-2σ<X<μ+2σ)=0.954,P(μ-3σ<X<μ+3σ)=0.997.根据行业标准,概率低于0.003视为小概率事件,工人随机将其中的8个交与质检员检验,则质检员认为设备需检修的概率为( )
101.7,100.3,99.6,102.4,98.2,103.2,101.1,98.8,100.4,100.0.
X~N(μ,σ2)有P(μ-2σ<X<μ+2σ)=0.954,P(μ-3σ<X<μ+3σ)=0.997.根据行业标准,概率低于0.003视为小概率事件,工人随机将其中的8个交与质检员检验,则质检员认为设备需检修的概率为( )
| A. | $\frac{44}{45}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{41}{45}$ |
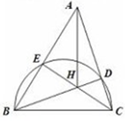 如图,以锐角△ABC的边BC为直径的半圆分别与AC、AB交于点D、E,BD、CE的交点为H,且BC=2.
如图,以锐角△ABC的边BC为直径的半圆分别与AC、AB交于点D、E,BD、CE的交点为H,且BC=2.