题目内容
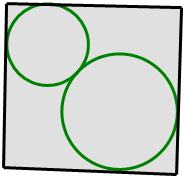 如图,在单位正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,记其中一个圆的半径为x,两圆的面积之和为S,将S表示为x的函数,求函数S=f(x)的解析式及f(x)的值域.
如图,在单位正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,记其中一个圆的半径为x,两圆的面积之和为S,将S表示为x的函数,求函数S=f(x)的解析式及f(x)的值域.考点:函数模型的选择与应用
专题:计算题
分析:首先设另一个圆的半径,通过分析两个圆内切时半径最大,从而求出定义域;然后根据图象分析面积之和的函数,并求出最大值和最小值.
解答:
解:设另一个圆的半径为y,则
x+x+
y+y=
⇒(
+1)(x+y)=
⇒x+y=
=2-
,
∴S=f(x)=π(x2+y2)=π[x2+(2-
-x)2]=π[2x2-2(2-
)x+(6-4
)]=π[2(x-
)2+(3-2
)],
因为当一个圆为正方形内切圆时半径最大,而另一圆半径最小,
所以函数的定义域为{x|
-
≤x≤
}
因为
∈[
-
,
],
所以Smin=π(3-2
);
因为f(
-
)=f(
)=
(3-2
),
所以Smax=
(3-2
),
所以函数S=f(x)的值域为[π(3-2
),
(3-2
)].
| 2 |
| 2 |
| 2 |
⇒(
| 2 |
| 2 |
⇒x+y=
| ||
|
| 2 |
∴S=f(x)=π(x2+y2)=π[x2+(2-
| 2 |
| 2 |
| 2 |
2-
| ||
| 2 |
| 2 |
因为当一个圆为正方形内切圆时半径最大,而另一圆半径最小,
所以函数的定义域为{x|
| 3 |
| 2 |
| 2 |
| 1 |
| 2 |
因为
2-
| ||
| 2 |
| 3 |
| 2 |
| 2 |
| 1 |
| 2 |
所以Smin=π(3-2
| 2 |
因为f(
| 3 |
| 2 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
所以Smax=
| 3π |
| 2 |
| 2 |
所以函数S=f(x)的值域为[π(3-2
| 2 |
| 3π |
| 2 |
| 2 |
点评:本题考查函数模型的选择与应用,通过对实际问题的分析,构造数学模型从而解决问题.这里需要对两圆关系进行仔细分析,防止误判.同时需要对知识熟练的掌握并应用,属于基础题.

练习册系列答案
相关题目
已知y=f(x)是偶函数,且在[0,+∞)上是减函数,则f(1-x2)是增函数的区间是( )
| A、[0,+∞) |
| B、(-∞,0] |
| C、[-1,0)∪(1,+∞) |
| D、(-∞,-1]∪(0,1] |
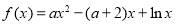 .
.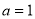 时,求曲线
时,求曲线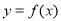 在点
在点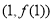 处的切线方程;
处的切线方程;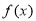 的单调区间;
的单调区间;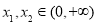 ,
,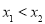 ,且
,且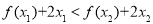 恒成立,求
恒成立,求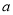 的取值范围.
的取值范围.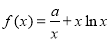 ,
,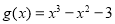
 的单调性
的单调性  ,使得
,使得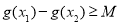 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数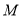
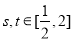 ,都有
,都有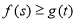 成立,求实数
成立,求实数 的取值范围
的取值范围