题目内容
cos2α+6sin2
-8sin4
= .
| α |
| 2 |
| α |
| 2 |
考点:三角函数的化简求值
专题:计算题
分析:利用二倍角公式,升角降次,化简表达式即可得到结果.
解答:
解:原式=cos2α+6
-8[
]2
=cos2α+3-3cosα-2(1-2cosα+cos2α)
=2cos2α-1+3-3cosα-2+4cosα-2cos2α
=cosα
故答案为:cosα
| 1-cosα |
| 2 |
| 1-cosα |
| 2 |
=cos2α+3-3cosα-2(1-2cosα+cos2α)
=2cos2α-1+3-3cosα-2+4cosα-2cos2α
=cosα
故答案为:cosα
点评:本题是基础题,灵活应用二倍角公式,注意升角降次的用法,在三角函数化简、求值、证明中经常应用.

练习册系列答案
相关题目
设ξ的概率密度函数为f(x)=
e-
,则下列结论错误的是( )
| 1 | ||
|
| (x-1)2 |
| 2 |
| A、p(ξ<1)=p(ξ>1) |
| B、p(-1≤ξ≤1)=p(-1<ξ<1) |
| C、f(x)的渐近线是x=0 |
| D、η=ξ-1~N(0,1) |
已知y=f(x)是偶函数,且在[0,+∞)上是减函数,则f(1-x2)是增函数的区间是( )
| A、[0,+∞) |
| B、(-∞,0] |
| C、[-1,0)∪(1,+∞) |
| D、(-∞,-1]∪(0,1] |
 =sin(2x+
=sin(2x+ )+ cos 2x.
)+ cos 2x.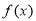 的单调递增区间。
的单调递增区间。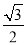 ,a=2,B=
,a=2,B=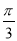 ,求△ABC的面积.
,求△ABC的面积.