题目内容
 如图,是一个奖杯的三视图(单位:cm),底座是正四棱台
如图,是一个奖杯的三视图(单位:cm),底座是正四棱台(V台=
| 1 |
| 3 |
| S上S下 |
(1)求这个奖杯的体积(保留π)
(2)求这个奖杯的全面积.(保留π)
考点:由三视图求面积、体积
专题:计算题
分析:三视图复原的几何体下部是底座是正四棱台,中部是圆柱,上部是球,根据三视图的数据,
(1)直径求出求这个奖杯的体积(保留π)
(2)求这个奖杯的全面积.(保留π)
(1)直径求出求这个奖杯的体积(保留π)
(2)求这个奖杯的全面积.(保留π)
解答:
解:三视图复原的几何体下部是底座是正四棱台,中部是圆柱,上部是球,
V=
h(S上+
+S下)+22π•16+
× 33=336+100π,(6分)
S=S上+S侧+S下+S柱侧+S球=12×12+
(12×4+6×4)×5+6×6+4π×16+4π32=360+100π(6分)
V=
| 1 |
| 3 |
| S上S下 |
| 4π |
| 3 |
S=S上+S侧+S下+S柱侧+S球=12×12+
| 1 |
| 2 |
点评:本题是基础题,考查几何体的三视图,几何体的表面积、体积的求法,准确判断几何体的形状是解题的关键.

练习册系列答案
相关题目
在任意的三个整数中,有且只有一个偶数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 为等差数列,且
为等差数列,且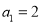 ,
,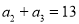 ,则
,则 ( )
( )