题目内容
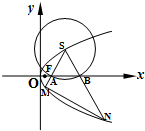 如图,已知点F是抛物线C:y2=x的焦点,S是抛物线C在第一象限内的点,且|SF|=
如图,已知点F是抛物线C:y2=x的焦点,S是抛物线C在第一象限内的点,且|SF|=| 5 |
| 4 |
(1)求点S的坐标;
(2)以S为圆心的动圆与x轴分别交于两点A,B,直线SA,SB分别交抛物线C于M,N两点,求直线MN的斜率.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设S(x0,y0)(y0>0),由已条件推导出|SF|=x0+
=
,由此能求出S点的坐标.
(2)设直线SA的方程为y-1=k(x-1),M(x1,y1),由
,求出M点坐标,设直线SB的斜率为-k,同理求出N点坐标,由此能求出直线MN的斜率.
| 1 |
| 4 |
| 5 |
| 4 |
(2)设直线SA的方程为y-1=k(x-1),M(x1,y1),由
|
解答:
解:(1)设S(x0,y0)(y0>0),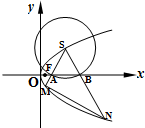
∵点F是抛物线C:y2=x的焦点,
S是抛物线C在第一象限内的点,且|SF|=
.
∴F(
,0),∴|SF|=x0+
=
,
∴x0=1,∴y0=1,
∴S点的坐标为(1,1).
(2)设直线SA的方程为y-1=k(x-1)(k≠0),
M(x1,y1),由
,得ky2-y+1-k=0,
解得:y1=1(舍),或y1=
-1,
∴M(
,
-1),
又由已知|SA|=|SB|得,直线SA与SB的斜率互为相反数,
∴直线SB的斜率为-k,同理得N(
,-
-1),
∴KMN=
=-
.
∴直线MN的斜率为-
.

∵点F是抛物线C:y2=x的焦点,
S是抛物线C在第一象限内的点,且|SF|=
| 5 |
| 4 |
∴F(
| 1 |
| 4 |
| 1 |
| 4 |
| 5 |
| 4 |
∴x0=1,∴y0=1,
∴S点的坐标为(1,1).
(2)设直线SA的方程为y-1=k(x-1)(k≠0),
M(x1,y1),由
|
解得:y1=1(舍),或y1=
| 1 |
| k |
∴M(
| (1-k)2 |
| k2 |
| 1 |
| k |
又由已知|SA|=|SB|得,直线SA与SB的斜率互为相反数,
∴直线SB的斜率为-k,同理得N(
| (1+k)2 |
| k2 |
| 1 |
| k |
∴KMN=
| ||||
|
| 1 |
| 2 |
∴直线MN的斜率为-
| 1 |
| 2 |
点评:本题考查抛物线上满足条件的点的坐标的求法,考查直线的斜率的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
若实数x,y满足
,则实数m=
的取值范围是( )
|
| y-1 |
| x+1 |
| A、(-1,1) | ||||
| B、[-1,1) | ||||
C、(-
| ||||
D、[-
|
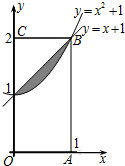 如图,在矩形OABC内:记抛物线y=x2+1与直线y=x+1围成的区域为M(图中阴影部分).随机往矩形OABC内投一点P,则点P落在区域M内的概率是( )
如图,在矩形OABC内:记抛物线y=x2+1与直线y=x+1围成的区域为M(图中阴影部分).随机往矩形OABC内投一点P,则点P落在区域M内的概率是( )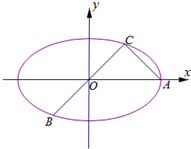 如图所示,已知A、B、C是长轴长为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且
如图所示,已知A、B、C是长轴长为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且 已知抛物线C:y2=2px(p>0)的准线方程为x=-2.
已知抛物线C:y2=2px(p>0)的准线方程为x=-2.