题目内容
如图(1),正方体ABCD-A1B1C1D1的棱长为2,点E1,F1分别是边A1B1、C1D1的中点.沿平面BCF1E1将正方体切割成左右两个几何体,再将右边的几何体补到左边,形成如图(2)的几何体.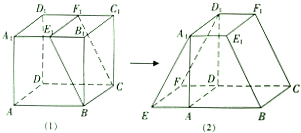
(1)判断直线A1F1与直线EC是否平行,并加于证明;
(2)求直线FD1与平面BCF1E1所成角的正弦值.

(1)判断直线A1F1与直线EC是否平行,并加于证明;
(2)求直线FD1与平面BCF1E1所成角的正弦值.
考点:直线与平面所成的角,直线与平面平行的性质
专题:空间位置关系与距离
分析:(Ⅰ)假设直线A1F1∥EC,过F1作CD的垂线,垂足为N,利用正方体的性质得到A1F1∥AN,得到AN∥EC,而AN与EC相交,得到矛盾;
(Ⅱ)连接AE1,过A作BE1的垂线,垂足为G,得到∠AE1G是直线FD1与平面BCF1E1所成角,计算即可.
(Ⅱ)连接AE1,过A作BE1的垂线,垂足为G,得到∠AE1G是直线FD1与平面BCF1E1所成角,计算即可.
解答:
解:(Ⅰ)直线A1F1与直线EC平行;
证明:假设直线A1F1∥EC,过F1,作CD的垂线,垂足为N,
因为上下底面平行,所以则A1F1∥AN,所以AN∥EC,与AN与EC相交矛盾,
所以假设不成立,即直线A1F1与直线EC不平行;
(Ⅱ)连接AE1,因为点E1,F1分别是边A1B1C1D1的中点,
AE1∥FD1,
过A作BE1的垂线,垂足为G,因为几何体是正方体ABCD-A1B1C1D1,
所以平面BCF1E1⊥平面ABE1A1,
所以AG⊥平面平面BCF1E1,
所以∠AE1G是直线FD1与平面BCF1E1所成角,
因为正方体棱长为2,所以AE1=BE1=
,AG=
,
所以sin∠AE1G=
=
=
,
所以直线FD1与平面BCF1E1所成角的正弦值
.
证明:假设直线A1F1∥EC,过F1,作CD的垂线,垂足为N,
因为上下底面平行,所以则A1F1∥AN,所以AN∥EC,与AN与EC相交矛盾,
所以假设不成立,即直线A1F1与直线EC不平行;
(Ⅱ)连接AE1,因为点E1,F1分别是边A1B1C1D1的中点,
AE1∥FD1,
过A作BE1的垂线,垂足为G,因为几何体是正方体ABCD-A1B1C1D1,
所以平面BCF1E1⊥平面ABE1A1,
所以AG⊥平面平面BCF1E1,
所以∠AE1G是直线FD1与平面BCF1E1所成角,
因为正方体棱长为2,所以AE1=BE1=
| 5 |
| 2×2 | ||
|
所以sin∠AE1G=
| AG |
| AE1 |
| ||||
|
| 4 |
| 5 |
所以直线FD1与平面BCF1E1所成角的正弦值
| 4 |
| 5 |
点评:本题考查了空间直线与直线的位置关系以及直线与平面所成的角的求法;关键是将空间角转为平面角.

练习册系列答案
相关题目
某几何体三视图如下图所示,则该几何体的表面积为( )


| A、16-π | B、16+π |
| C、16-2π | D、16+2π |
已知集合M={x|
≤1},N={x|y=lg(1-x)},则下列关系中正确的是( )
| 1 |
| x |
| A、(∁RM)∩N=∅ |
| B、M∪N=R |
| C、M?N |
| D、(∁RM)∪N=R |
若sinα=
,cos(α+β)=-
,且α,β是锐角,则β等于( )
4
| ||
| 7 |
| 11 |
| 14 |
A、
| ||
B、
| ||
C、
| ||
D、
|
不等式x2-2x-3>0的解集是( )
| A、(-1,3) |
| B、(3,+∞) |
| C、(-∞,-1)∪(3,+∞) |
| D、(-∞,-1) |
