题目内容
某种产品的广告费支出x与销售额y (单位:百万元)之间有如下的对应数据:
根据上表提供的数据 算出
=5,
=50,
xi2=145,
xiyi=1390用最小二乘法求出y关于x的线性回归方程为 .
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |
. |
| x |
. |
| y |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
考点:线性回归方程
专题:概率与统计
分析:根据横标和纵标的平均数,得到这组数据的样本中心点,利用最小二乘法求出线性回归方程的系数,代入样本中心点求出a的值,写出线性回归方程.
解答:
解:∵
=5,
=50,
xi2=145,
xiyi=1390,
∴
=
=
=
=7,
=
-7
=50-7×5=15,
故线性回归方程为:
=7x+15;
故答案为:
=7x+15
. |
| x |
. |
| y |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
∴
| ? |
| b |
| |||||||
|
| 1390-5×5×50 |
| 145-5×52 |
| 140 |
| 20 |
| ? |
| a |
. |
| y |
. |
| x |
故线性回归方程为:
| ? |
| y |
故答案为:
| ? |
| y |
点评:本题考查线性回归方程的求法和应用,本题解题的关键是利用最小二乘法求出线性回归方程的系数,这是解答正确的主要环节.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
在△ABC中,“sinA>
”是“A>
”的( )
| ||
| 2 |
| π |
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
抛物线y2=4x上与焦点相距最近的点的坐标是( )
| A、(0,0) |
| B、(1,2) |
| C、(1,-2) |
| D、以上都不是 |
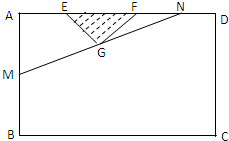 某小区想利用一矩形空地ABCD建造市民健身广场,设计时决定保留空地边上的一个水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中AD=60m,AB=40m,且△EFG中,∠EGF=90°,经测量得到AE=10m,EF=20m.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点G作一条直线交AB,DF于M,N,从而得到五边形MBCDN的市民健身广场.
某小区想利用一矩形空地ABCD建造市民健身广场,设计时决定保留空地边上的一个水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中AD=60m,AB=40m,且△EFG中,∠EGF=90°,经测量得到AE=10m,EF=20m.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点G作一条直线交AB,DF于M,N,从而得到五边形MBCDN的市民健身广场.