题目内容
11.在△ABC中,sin2A十sin2B十sin2C=2$\sqrt{3}$sinAsinBsinC,则△ABC的形状是( )| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 正三角形 |
分析 由于sin2A+sin2B+sin2C=2$\sqrt{3}$sinAsinBsinC,利用正弦定理可得:a2+b2+c2=2$\sqrt{3}$absinC,由余弦定理可得:a2+b2-c2=2abcosC,利用sin2C+cos2C=$\frac{({a}^{2}+{b}^{2}+{c}^{2})^{2}}{12{a}^{2}{b}^{2}}$+$\frac{({a}^{2}+{b}^{2}-{c}^{2})^{2}}{4{a}^{2}{b}^{2}}$=1,化简即可得出.
解答 解:∵sin2A+sin2B+sin2C=2$\sqrt{3}$sinAsinBsinC,
由正弦定理可得:a2+b2+c2=2$\sqrt{3}$absinC,
由余弦定理可得:a2+b2-c2=2abcosC,
∴sin2C+cos2C=$\frac{({a}^{2}+{b}^{2}+{c}^{2})^{2}}{12{a}^{2}{b}^{2}}$+$\frac{({a}^{2}+{b}^{2}-{c}^{2})^{2}}{4{a}^{2}{b}^{2}}$=1,
化为(a2-b2)2+(b2-c2)2+(a2-c2)2=0,
∴a=b=c.
∴△ABC是正三角形.
故选:D.
点评 本题考查了正弦定理余弦定理、同角三角函数基本关系式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.已知λ∈R,向量$\overrightarrow{a}$=( 3,λ ),$\overrightarrow{b}$=(λ-1,2),则“λ=$\frac{3}{5}$”是“$\overrightarrow{a}$⊥$\overrightarrow{b}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.已知点M(0,$\sqrt{15}$)及抛物线y2=4x上一动点N(x,y),则x+|MN|的最小值为( )
| A. | $\sqrt{5}$ | B. | $2\sqrt{3}$ | C. | 3 | D. | 4 |
6.全集U=R,集合A={x|2x2-x-1>0},B={x|-1≤x≤2,x∈Z},则图中阴影部分所表示的集合为( )
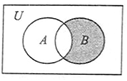

| A. | {-1,2} | B. | {-1,0} | C. | {0,1} | D. | {1,2} |
3.函数f(x)=2|sinx|的最小正周期为( )
| A. | 2π | B. | $\frac{3π}{2}$ | C. | π | D. | $\frac{π}{2}$ |
1.已知z=$\frac{1-3i}{3+i}$(i为虚数单位),则z的共轭复数的虚部为( )
| A. | -i | B. | i | C. | -1 | D. | 1 |