题目内容

16．经过原点且到点A（1，1）的距离是$\sqrt{2}$的直线方程为x+y=0．．

分析 由题意可知：直线的斜率存在，设直线方程为：y=kx，利用点到直线的距离公式即可得出．

解答 解：由题意可知：直线的斜率存在，设直线方程为：y=kx，
则$\frac{|k-1|}{\sqrt{{k}^{2}+1}}$=$\sqrt{2}$，化为：k=-1．
∴要求的直线方程为：y+x=0．
故答案为：y+x=0．

点评 本题考查了直线方程、点到直线的距离公式，考查了推理能力 与计算能力，属于基础题．

练习册系列答案
相关题目
8．某小商品2016年的价格为15元/件，你那销量为a件，现经销商计划在2017年该商品的价格降至10元/件到14元/件之间，经调查，顾客的期望价格为7元/件，经市场调查，该商品的价格下降后增加的销售量与定价和顾客期望价格的差成反比，比例系数为k，该商品的成本价为5元/件．
（1）写出该商品价格下降后，经销商的年收益y与定价x的函数关系式；
（2）设k=3a，当定价为多少时，经销商2017年的收益恰是2016年收益的1.2倍？
9．定义在 R 上的奇函数 f （x） 满足 f （2+x ）=f （2-x），且 f （1）=1，则 f （2017）=（　　）
A．0B．1C．-1D．-2
4．已知二次函数y=f（x）的图象向上平移2个单位长度，再向右平移1个单位长度，得到函数y=-2x2+4x+1的图象，则f（x）的函数解析式为（　　）
A．f（x）=-2x2+1B．f（x）=-2（x+1）2+2C．f（x）=-2（x-3）2+4D．f（x）=-2（x-2）2+5
11．在△ABC中，sin2A十sin2B十sin2C=2$\sqrt{3}$sinAsinBsinC，则△ABC的形状是（　　）
A．直角三角形B．锐角三角形C．钝角三角形D．正三角形
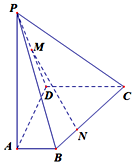1．如图，在四棱锥P-ABCD中，侧棱PA⊥底面ABCD，底面ABCD是直角梯形，AD⊥AB，AB∥DC，AD=DC=AP=2，AB=1，点M为PD的中点，点N是为棱CB上一点，且$\overrightarrow{BN}=λ\overrightarrow{BC}，λ∈（{0，1}）$．
（Ⅰ）判断直线MN能否垂直于直线AD，若能，确定N点的位置，若不能，请说明理由；
（Ⅱ）若直线MN⊥BC，求二面角M-AN-C的余弦值．
8．在直角坐标系中xOy中，已知曲线E经过点P（1，$\frac{2\sqrt{3}}{3}$），其参数方程为$\left\{\begin{array}{l}{x=acosα}\\{y=\sqrt{2}sinα}\end{array}\right.$（α为参数），以原点O为极点，x轴的正半轴为极轴建立极坐标系．
（1）求曲线E的极坐标方程；
（2）若直线l交E于点A、B，且OA⊥OB，求证：$\frac{1}{|OA{|}^{2}}$+$\frac{1}{|OB{|}^{2}}$为定值，并求出这个定值．
5．如果两组数a1，a2，…an和b1，b2，…bn的平均数分别是a和b，那么一组数a1+3b1，a2+3b2，…，an+3bn的平均数是a+3b．
6．在△ABC中，D为BC边上一点，且满足$\overrightarrow{AD}$=$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$），BC=10，AD=12，且$\overrightarrow{AD}$•$\overrightarrow{BC}$=0，则$\overrightarrow{AD}$•$\overrightarrow{AC}$=（　　）
A．144B．100C．169D．60

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网