题目内容
1.已知函数f(x)=x2+(a+1)x+b,且f(3)=3,又知f(x)≥x恒成立,求a,b的值.分析 根据二次函数的性质得到关于a,b的方程,联立解方程组,求出a,b的值即可.
解答 解:由f(3)=3得:9+3(a+1)+b=3①,
由f(x)≥x恒成立,即x2+ax+b≥0恒成立,
得:△=a2-4b=0②,
由①②解得:a=-6,b=9.
点评 本题考查了二次函数的性质,考查函数恒成立问题,是一道基础题.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
3.某几何体的三视图如图所示,则该几何体的表面积为( )


| A. | 2π+12 | B. | π+12 | C. | 2π+24 | D. | π+24 |
13.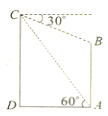 如图,在热气球C正前方有一高为m的建筑物AB,在建筑物底部A测得C的仰角为60°,同时在C处测得建筑物顶部B的仰角为30°,则此时热气球的高度CD为( )
如图,在热气球C正前方有一高为m的建筑物AB,在建筑物底部A测得C的仰角为60°,同时在C处测得建筑物顶部B的仰角为30°,则此时热气球的高度CD为( )
 如图,在热气球C正前方有一高为m的建筑物AB,在建筑物底部A测得C的仰角为60°,同时在C处测得建筑物顶部B的仰角为30°,则此时热气球的高度CD为( )
如图,在热气球C正前方有一高为m的建筑物AB,在建筑物底部A测得C的仰角为60°,同时在C处测得建筑物顶部B的仰角为30°,则此时热气球的高度CD为( )| A. | $\sqrt{2}m$ | B. | $\sqrt{3}m$ | C. | $\frac{{3\sqrt{3}}}{2}m$ | D. | $\frac{3}{2}m$ |
11.已知幂函数f(x)=λ•xα的图象过点$P(\frac{1}{2},\frac{{\sqrt{2}}}{2})$,则λ+α=( )
| A. | 2 | B. | 1 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |