题目内容
14．在△ABC中，角A，B，C的对边分别为a，b，c．a=15，b=10，A=60°，则sinB=$\frac{\sqrt{3}}{3}$．分析 由已知利用正弦定理即可求值得解．
解答 解：∵a=15，b=10，A=60°，
∴sinB=$\frac{bsinA}{a}$=$\frac{10×\frac{\sqrt{3}}{2}}{15}$=$\frac{\sqrt{3}}{3}$．
故答案为：$\frac{\sqrt{3}}{3}$．
点评 本题主要考查了正弦定理的应用，属于基础题．
练习册系列答案
相关题目
4．设函数f（x）=sinωx（ω＞0），将f（x）的图象向左平移$\frac{π}{6}$个单位长度后，所得的图象与y=cosωx的图象重合，则ω的最小值等于（ ）
| A． | $\frac{1}{3}$ | B． | 3 | C． | 6 | D． | 9 |
9．若变量x，y满足约束条件$\left\{\begin{array}{l}x+y≤2\\ x≥1\\ y≥0\end{array}\right.$，则z=2x+y的最大值为（ ）
| A． | 0 | B． | 2 | C． | 3 | D． | 4 |
6．已知四面体ABCD的侧面展开图如图所示，则其体积为（ ）
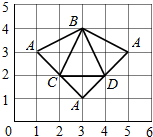
| A． | 2 | B． | $\frac{3}{2}$ | C． | $\frac{3}{4}$ | D． | $\frac{2}{3}$ |
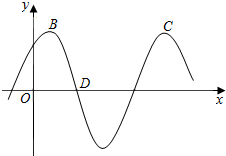如图所示，B，C两点是函数f（x）=Asin（2x+$\frac{π}{3}$）（A＞0）图象上相邻的两个最高点，D点为函数f（x）图象与x轴的一个交点．