Question

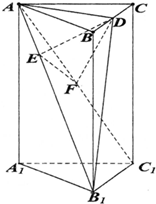如图，正三棱柱ABC-A₁B₁C₁底面边长为2，AA₁=4

2

，AC₁=2AF，AD⊥B₁D，AE=

1

2

B₁E．
（1）证明：DF∥平面ABB₁A₁；
（2）求三棱锥A-DEF的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,直线与平面平行的判定

专题：综合题,空间位置关系与距离

分析：（1）证明D为BC的中点，DF∥A₁B，即可证明DF∥平面ABB₁A₁；
（2）利用V_A-DEF=V_D-AEF=

1

6

V_D-AB1C1=V_A-DB1C1，求三棱锥A-DEF的体积．

解答： （1）证明：如图：连接A₁B，A₁C
∵ABC-A₁B₁C₁是正三棱柱，∴AD⊥B₁D，AD⊥BB₁
∴AD⊥平面BB₁C₁，
∵△ABC为正三角形，
∴D为BC的中点，
∵F为AC₁的中点，
∴DF∥A₁B，
∵DF?平面ABB₁A₁，A₁B?平面ABB₁A₁，
∴DF∥平面ABB₁A₁；
（2）解：V_A-DEF=V_D-AEF=

1

6

V_D-AB1C1=V_A-DB1C1=

1

3

•

1

6

•S△B1C1D•AD=

2 6

9

．

点评：证明线面平行关键是在平面内找到一条直线与已知直线平行；求三棱锥的体积时若不易求出一般是先观察一下是否换一个底面积与高都容易求的定点．