题目内容
已知数列{an}是一个等差数列,其前n项和为Sn,且a2=1,S5=-5.
(Ⅰ)求通项公式an;
(Ⅱ)求数列前n项和Sn,并求出Sn的最大值.
(Ⅲ)求数列{|an|}的前n项和Tn.
(Ⅰ)求通项公式an;
(Ⅱ)求数列前n项和Sn,并求出Sn的最大值.
(Ⅲ)求数列{|an|}的前n项和Tn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)利用等差数列通项公式解方程组;(Ⅱ)等差数列求和公式;(Ⅲ)利用等差数列求和公式;注意对项的符号的判断.
解答:
解:(Ⅰ)设{an}的公差为d,由已知条件,
,解出a1=3,d=-2.
所以an=a1+(n-1)d=-2n+5. …(4分)
(Ⅱ)Sn=na1+
d=-n2+4n=4-(n-2)2. …(6分)
所以n=2时,Sn取到最大值4. …(8分)
(Ⅲ)令an=-2n+5>0,则n<
.∴|an|=
当1≤n≤2时,Tn=a1+a2+…+an=-n2+4n…(10分)
当n≥3时,Tn=a1+a2-(a3+a4+…+an)=S2-(Sn-S2)=2S2-Sn=n2-4n+8
综上所述:Tn=
…(12分)
|
所以an=a1+(n-1)d=-2n+5. …(4分)
(Ⅱ)Sn=na1+
| n(n-1) |
| 2 |
所以n=2时,Sn取到最大值4. …(8分)
(Ⅲ)令an=-2n+5>0,则n<
| 5 |
| 2 |
|
当1≤n≤2时,Tn=a1+a2+…+an=-n2+4n…(10分)
当n≥3时,Tn=a1+a2-(a3+a4+…+an)=S2-(Sn-S2)=2S2-Sn=n2-4n+8
综上所述:Tn=
|
点评:本题考查了等差数列的通项公式,求和公式的应用,注意题目条件,确定数列的特点是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
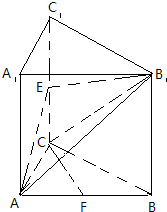 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,F是AB的中点,AC=BC=1,AA1=2.
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,F是AB的中点,AC=BC=1,AA1=2.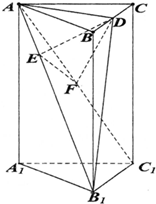 如图,正三棱柱ABC-A1B1C1底面边长为2,AA1=4
如图,正三棱柱ABC-A1B1C1底面边长为2,AA1=4