题目内容
观察以下各式：
sin230°+cos260°+sin30°cos60°=
sin220°+cos250°+sin20°cos50°=
sin215°+cos245°+sin15°cos45°=
sin25°+cos235°+sin5°cos35°=
分析以上各式的共同特点，则具有一般规律的等式为 ．
sin230°+cos260°+sin30°cos60°=
| 3 |
| 4 |
sin220°+cos250°+sin20°cos50°=
| 3 |
| 4 |
sin215°+cos245°+sin15°cos45°=
| 3 |
| 4 |
sin25°+cos235°+sin5°cos35°=
| 3 |
| 4 |
分析以上各式的共同特点，则具有一般规律的等式为
考点：归纳推理
专题：推理和证明
分析：我们可以发现等式左边余弦均为正弦度数加30°，右边是常数，由此不难得到结论．
解答：
解：观察以下各式：
∵sin230°+cos260°+sin30°cos60°=
，sin220°+cos250°+sin20°cos50°=
，
∴sin230°+cos2（30°+30°）+sin30°cos（30°+30°）=
，sin220°+cos2（20°+30°）+sin20°cos（20°+30°）=
，
于是根据各式的共同特点，则具有一般规律的等式可得出sin2α+cos2(α+30°)+sinαcos(α+30°)=
．
故答案为：sin2α+cos2(α+30°)+sinαcos(α+30°)=
．
∵sin230°+cos260°+sin30°cos60°=
| 3 |
| 4 |
| 3 |
| 4 |
∴sin230°+cos2（30°+30°）+sin30°cos（30°+30°）=
| 3 |
| 4 |
| 3 |
| 4 |
于是根据各式的共同特点，则具有一般规律的等式可得出sin2α+cos2(α+30°)+sinαcos(α+30°)=
| 3 |
| 4 |
故答案为：sin2α+cos2(α+30°)+sinαcos(α+30°)=
| 3 |
| 4 |
点评：本题主要考查了归纳推理，通过观察个别情况发现某些相同性质，从已知的相同性质中推出一个明确表达的一般性命题（猜想），属基础题．
练习册系列答案
名校课堂系列答案
相关题目
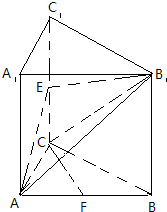如图，三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC，∠ACB=90°，E是棱CC1的中点，F是AB的中点，AC=BC=1，AA1=2．
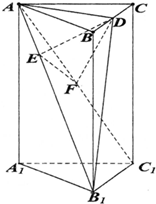如图，正三棱柱ABC-A1B1C1底面边长为2，AA1=4