题目内容
5.在△ABC中,角A,B,C的对边分别为a,b,c.已知2cosA(bcosC+ccosB)=a.(1)求角A的值;
(2)若$cosB=\frac{3}{5}$,求sin(B-C)的值.
分析 (1)由正弦定理化简已知等式可得2cosAsinA=sinA,结合sinA≠0,可求$cosA=\frac{1}{2}$,结合范围A∈(0,π),可求A的值.
(2)由已知利用同角三角函数基本关系式可求sinB,利用倍角公式可求sin2B,cos2B,由sin(B-C)=sin(2B-$\frac{2π}{3}$),利用两角差的正弦函数公式即可计算得解.
解答 (本题满分为14分)
解:(1)由正弦定理可知,2cosA(sinBcosC+sinCcosB)=sinA,…(2分)
即2cosAsinA=sinA,
因为A∈(0,π),
所以sinA≠0,
所以2cosA=1,即$cosA=\frac{1}{2}$,…(4分)
又A∈(0,π),
所以$A=\frac{π}{3}$. …(6分)
(2)因为$cosB=\frac{3}{5}$,B∈(0,π),
所以$sinB=\sqrt{1-{{cos}^2}B}=\frac{4}{5}$,…(8分)
所以$sin2B=2sinBcosB=\frac{24}{25}$,$cos2B=1-2{sin^2}B=-\frac{7}{25}$,…(10分)
所以$sin(B-C)=sin[B-(\frac{2π}{3}-B)]=sin(2B-\frac{2π}{3})$=$sin2Bcos\frac{2π}{3}-cos2Bsin\frac{2π}{3}$…(12分)
=$-\frac{24}{25}×\frac{1}{2}-(-\frac{7}{25})×\frac{{\sqrt{3}}}{2}$=$\frac{{7\sqrt{3}-24}}{50}$.…(14分)
点评 本题主要考查了正弦定理,同角三角函数基本关系式,倍角公式,两角差的正弦函数公式在解三角形中的应用,考查了计算能力和转化思想,属于中档题.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案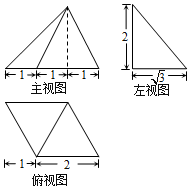
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{{4\sqrt{3}}}{3}$ | C. | 2 | D. | $\frac{{5\sqrt{3}}}{3}$ |
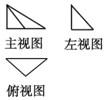 一个高为2的三棱锥的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,则该几何体外接球的体积( )
一个高为2的三棱锥的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,则该几何体外接球的体积( )| A. | 12π | B. | 9π | C. | $4\sqrt{3}π$ | D. | $\sqrt{3}π$ |
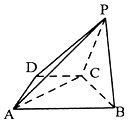 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$,平面PBC⊥平面ABCD.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$,平面PBC⊥平面ABCD. 某次比赛甲得分的茎叶图如图所示,若去掉一个最高分,去掉一个最低分,则剩下4个分数的方差为14.
某次比赛甲得分的茎叶图如图所示,若去掉一个最高分,去掉一个最低分,则剩下4个分数的方差为14.