题目内容
15.已知p:(x+2)(x-2)≤0.q:x2-3x-4≤0,若p∧q为假,p∨q为真.求实数x的取值范围.分析 若p∧q为假,p∨q为真.则命题p,q一真一假,进而可得实数x的取值范围.
解答 解:解(x+2)(x-2)≤0得:x∈[-2,2],
故命题p:x∈[-2,2].
解x2-3x-4≤0得:x∈[-1,4],
故命题q:x∈[-1,4],
若p∧q为假,p∨q为真.
则命题p,q一真一假,
当p真q假时,x∈[-2,-1),
当p假q真时,x∈(2,4],
综上可得实数x的取值范围为:[-2,-1)∪(2,4].
点评 本题以命题的真假判断与应用为载体,考查了复合命题,二次不等式的解法等知识点,难度中档.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
10.执行如图所示的程序框图,则输出的结果为( )


| A. | 10 | B. | 17 | C. | 24 | D. | 26 |
3.函数f(x)=$\sqrt{(\frac{1}{3})^{x}-2}$的定义域为( )
| A. | (-∞,log32] | B. | (-∞,-log32] | C. | [log32,+∞) | D. | [-log32,+∞) |
 如图,在半径为30cm的半圆形铁皮上截取一块矩形材料ABCD(点A,B在直径上,点C,D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗).
如图,在半径为30cm的半圆形铁皮上截取一块矩形材料ABCD(点A,B在直径上,点C,D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗).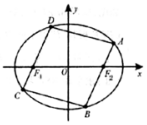 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴的一个顶点与两个焦点构成正三角形,且该三角形的周长为6
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴的一个顶点与两个焦点构成正三角形,且该三角形的周长为6