题目内容
已知x＞1，则函数f（x）=4x+
+1的最小值是（ ）
| 1 |
| x-1 |
| A、7 | B、9 | C、11 | D、13 |
考点：基本不等式
专题：不等式的解法及应用
分析：把函数恒等变形f（x）=4x+
+1=4（x-1）+
+5，利用均值不等式求解．
| 1 |
| x-1 |
| 1 |
| x-1 |
解答：
解：函数f（x）=4x+
+1=4（x-1）+
+5
∵x＞1，∴x-1＞0，
∴4（x-1）+
≥4，（x=
等号成立）
4（x-1）+
+5≥9（x=
等号成立）
故选：B
| 1 |
| x-1 |
| 1 |
| x-1 |
∵x＞1，∴x-1＞0，
∴4（x-1）+
| 1 |
| x-1 |
| 3 |
| 2 |
4（x-1）+
| 1 |
| x-1 |
| 3 |
| 2 |
故选：B
点评：本题考查了均值不等式在函数最值中的应用，属于容易题．
练习册系列答案
相关题目
下列命题中的假命题是（ ）
A、?x∈R，sinx=
| ||||
| B、?x∈R，log2x=1 | ||||
C、?x∈R，(
| ||||
| D、?x∈R，x2≥0 |
函数f（x）=-x2+2ax+3在区间（-∞，4）上单调递增，则a的取值范围是（ ）
| A、a＜4 | B、a≤4 |
| C、a＞4 | D、a≥4 |
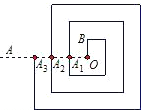如图是一回形图，其回形通道的宽和OB的长均为1，回形线与射线OA交于A1、A2、