题目内容
5.已知定义在R上的奇函数f(x)在[0,+∞)上递减,若f(x3-2x+a)<f(x+1)对x∈[-1,2]恒成立,则a的取值范围为( )| A. | (-3,+∞) | B. | (-∞,-3) | C. | (3,+∞) | D. | (-∞,3) |
分析 由题意可得f(x)在(-∞,+∞)上是减函数,当x∈[-1,2]时,x3-2x+a>(x+1)恒成立,即a>-x3+3x+1恒成立.利用导数求得g(x)=-x3+3x+1的最大值,可得a的取值范围.
解答 解:∵定义在R上的奇函数f(x)在[0,+∞)上递减,故f(x)在(-∞,+∞)上是减函数,
若f(x3-2x+a)<f(x+1)对x∈[-1,2]恒成立,则当x∈[-1,2]时,x3-2x+a>x+1恒成立,
即a>-x3+3x+1恒成立.
令g(x)=-x3+3x+1,令g′(x)=-3x2+3=0,x=±1,在[-1,1]上,g′(x)>0,g(x)是增函数;
在(1,2]上,g′(x)<0,g(x)是减函数,故g(x)的最大值为g(1)=3,∴a>3,
故选:C.
点评 本题考查的知识点是函数的单调性,函数的奇偶性,函数恒成立问题,利用导数求函数的最值,是函数图象和性质的综合应用,属于中档题.

练习册系列答案
相关题目
14.如图,在长方形OABC内任取一点P(x,y),则点P落在阴影部分的概率为( )

| A. | $1-\frac{3}{2e}$ | B. | $1-\frac{1}{2e}$ | C. | $1-\frac{2}{e}$ | D. | $1-\frac{1}{e}$ |
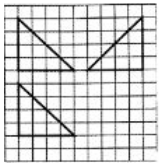 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的各个顶点在某一个球面上,则该球面的表面积为48π.
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的各个顶点在某一个球面上,则该球面的表面积为48π.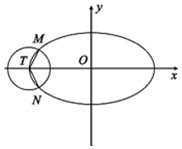 如图已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,以椭圆的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M,N.
如图已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,以椭圆的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M,N.