题目内容
17.已知方程${x^2}+3\sqrt{3}x+4=0$有两个实根x1,x2,记α=arctanx1,β=arctanx2,求α+β的值.分析 由条件利用韦达定理求得x1+x2 =-3$\sqrt{3}$,x1•x2=4,α+β∈(0,π),再利用两角和的正切公式求得tan(α+β)的值,可得α+β的值.
解答 解:由x1、x2是方程x2+3$\sqrt{3}$x+4=0的两根,可得x1+x2 =-3$\sqrt{3}$,x1•x2=4,
故x1、x2均大于零,故arctanx1+arctanx2∈(0,π),即α+β∈(0,π),
∵α=arctanx1,β=arctanx2,
∴tanα=x1,tanβ=x2,
∴tan(α+β)=$\frac{{x}_{1}+{x}_{2}}{1-{x}_{1}{x}_{2}}$=$\sqrt{3}$,
∴α+β=$\frac{π}{3}$.
点评 本题主要考查韦达定理,两角和的正切公式,属于中档题.

练习册系列答案
相关题目
5.已知定义在R上的奇函数f(x)在[0,+∞)上递减,若f(x3-2x+a)<f(x+1)对x∈[-1,2]恒成立,则a的取值范围为( )
| A. | (-3,+∞) | B. | (-∞,-3) | C. | (3,+∞) | D. | (-∞,3) |
7.已知某几何体的三视图如图所示,则该几何体的内切球的表面积为( )
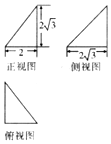

| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | 3π | D. | 4π |
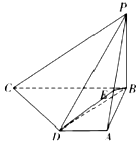 如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA.
如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA.