题目内容
14.如图,在长方形OABC内任取一点P(x,y),则点P落在阴影部分的概率为( )
| A. | $1-\frac{3}{2e}$ | B. | $1-\frac{1}{2e}$ | C. | $1-\frac{2}{e}$ | D. | $1-\frac{1}{e}$ |
分析 根据几何概型的特点,首先利用定积分表示阴影部分的面积,利用面积比求概率.
解答 解:由已知B在y=ax上,所以a=e,得到阴影部分的面积为${∫}_{0}^{1}({e}^{x}-1)dx+\frac{1}{2}×1×1$=(ex-x)|${\;}_{0}^{1}$+$\frac{1}{2}$=e-$\frac{3}{2}$,
长方形的面积为1×e=e,由几何概型的公式得到$\frac{e-\frac{3}{2}}{e}=1-\frac{3}{2e}$;
故选A.
点评 本题考查了定积分的应用以及几何概型的概率求法;正确表示阴影部分的面积是解答本题的关键.

练习册系列答案
相关题目
4.已知不等式$\sqrt{2}$sin$\frac{x}{4}$cos$\frac{x}{4}$+$\sqrt{6}$cos2$\frac{x}{4}$-$\frac{\sqrt{6}}{2}$-m≥0对于x∈[-$\frac{π}{3}$,$\frac{π}{3}$]恒成立,则实数m的取值范围是( )
| A. | (-∞,-$\sqrt{2}$] | B. | (-∞,$\frac{\sqrt{2}}{2}$] | C. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$] | D. | [$\sqrt{2}$,+∞) |
5.已知定义在R上的奇函数f(x)在[0,+∞)上递减,若f(x3-2x+a)<f(x+1)对x∈[-1,2]恒成立,则a的取值范围为( )
| A. | (-3,+∞) | B. | (-∞,-3) | C. | (3,+∞) | D. | (-∞,3) |
4.设等差数列{an}的公差d≠0,且a2=-d,若ak是a6与ak+6的等比中项,则k=( )
| A. | 5 | B. | 6 | C. | 9 | D. | 11 |
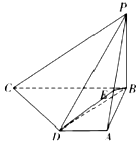 如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA.
如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA.