题目内容
已知点P是抛物线y2=2x上的一个动点,过点P作圆(x-3)2+y2=1的一条切线,切点为M,则|PM|的取值范围是 .
考点:圆与圆锥曲线的综合,圆的切线方程
专题:函数的性质及应用,圆锥曲线的定义、性质与方程
分析:根据题意,利用等面积可得|MN|=2|ME|,所以当|PO1|最小时,|MN|取最小值,故可求.
解答:
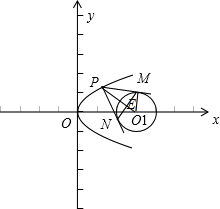 解:设圆心为O1(3,0),PO1与MN交于E,
解:设圆心为O1(3,0),PO1与MN交于E,
则|PO1|2=|PM|2+1,
由等面积可知:|MN|=2|ME|=
=
=
=2
,
则当|PO1|最小时,|MN|取最小值,|PO1|=
=
=
,
则当x=2时,|PO1|有最小值
,
故|MN|最小值是|MN|═2
=
.
则|PM|的取值范围是:[
,+∞).
故答案为:[
,+∞).
 解:设圆心为O1(3,0),PO1与MN交于E,
解:设圆心为O1(3,0),PO1与MN交于E,则|PO1|2=|PM|2+1,
由等面积可知:|MN|=2|ME|=
| 2|PM||O1M| |
| |PO1| |
| 2|PM| |
| |PO1| |
2
| ||
| |PO1| |
1-
|
则当|PO1|最小时,|MN|取最小值,|PO1|=
| (x-3)2+y2 |
=
| (x-3)2+2x |
| (x-2)2+5 |
则当x=2时,|PO1|有最小值
| 5 |
故|MN|最小值是|MN|═2
1-
|
4
| ||
| 5 |
则|PM|的取值范围是:[
4
| ||
| 5 |
故答案为:[
4
| ||
| 5 |
点评:本题重点考查圆与抛物线的综合,考查距离最小值的求解,解题的关键是利用等面积可得|MN|=2|ME|=2
,考查化简运算能力,考查转化思想.
1-
|

练习册系列答案
相关题目
已知x1、x2是函数f(x)=
x2+
ax2+2bx(a,b∈R)的两个极值点,且x1∈(0,1),x2∈(1,2),则4a+3b的取值范围是( )
| 1 |
| 3 |
| 1 |
| 2 |
| A、(-9,-4) |
| B、(-8,-4) |
| C、(-9,-8) |
| D、(-15,-4) |
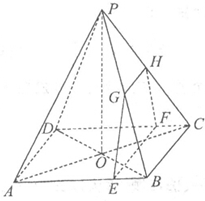 如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2
如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2