Question

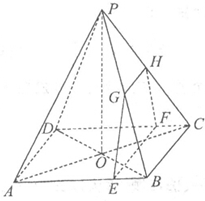如图，四棱锥P-ABCD的底面是边长为8的正方形，四条侧棱长均为2

17

，AC、BD交于O点，点G，E，F，H分别是棱PB，AB，CD，PC上共面的四点，平面GEFH⊥平面ABCD，BC∥平面GEFH．
（Ⅰ）证明：PO⊥平面ABCD；
（Ⅱ）GH∥EF；
（Ⅲ）若EB=2，求四边形GEFH的面积．

Answer 1

考点：直线与平面垂直的判定,棱柱、棱锥、棱台的侧面积和表面积,直线与平面平行的性质

专题：空间位置关系与距离

分析：（Ⅰ）首先，AC、BD交于点O，结合△PAC和△PBD均为等腰三角形，从而得到结果；
（Ⅱ）首先，可以结合条件，得到BC∥EF，然后，BC∥GH，即得证明；
（Ⅲ）设BD与EF交于点K，连接GK，得到PO∥GK，K为靠近点BD的四等分点，然后，得证．

解答： 解：（Ⅰ）∵四边形ABCD为正方形，且AC、BD交于点O，
∴O为AC、BD的中点，由已知得
PA=PC，PB=PD，
△PAC和△PBD均为等腰三角形，
∴PO⊥AC，PO⊥BD，
又AC、BD?平面ABCD，且AC∩BD=O，
∴PO⊥平面ABCD，
（Ⅱ）∵BC∥平面GEFH，
BC?平面ABCD，平面GEFH∩平面ABCD=EF，
∴BC∥EF，
同理可得，BC∥GH，
∴GH∥EF，
（Ⅲ）设BD与EF交于点K，连接GK，
∵PO⊥平面ABCD，且PO?平面GEFH，
∴PO∥平面GEFH，又平面GEFH∩平面PBD=GK，PO?平面PBD，
∴PO∥GK，
∴GK为四边形GEFH底边上的高，
又因为BE=2，AB=8，得点E是靠近B点的AB的四等分点，
∵KE∥AD，
∴K为靠近点BD的四等分点，
∴K为OB的中点，又PO∥GK，
∴G为PB的中点，又GH∥BC，
∴H为PC的中点，又BC=8，
∴GH=4，又由已知得PB=2

17

，OB=4

2

，
∴PO=

PB2-OB2

=

68-32

=6，
∴GK=

1

2

PO=3，
又由BC∥EF，BE∥GK，可得EF=8，
∴S=

1

2

（GH+EF）•GK=

1

2

•（4+8）•3=18，

点评：本题重点考查了空间中直线与直线平行和垂直、直线与平面平行和垂直、平面和平面平行和垂直的性质和判定等知识，属于中档题．