题目内容
已知函数f（x）=[x2+（2a-2）x+2-2a-b]ex（a，b∈R）在区间[-1，3]上是减函数，则a+b的最小值是（ ）
| A、4 | ||
| B、2 | ||
C、
| ||
D、
|
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：根据导数的运算法则吗，先求导，再根据区间[-1，3]上是减函数，得到即
，再利用线性区域，求的最值．
|
解答：
解：∵f（x）=[x2+（2a-2）x+2-2a-b]ex（a，b∈R）在区间[-1，3]上是减函数，
∴f′（x）=ex（x2+2ax-b）＜0，
∴x2+2ax-b＜0，令g（x）=x2+2ax-b，
∵f（x）=[x2+（2a-2）x+2-2a-b]ex（a，b∈R）在区间[-1，3]上是减函数，
∴
，
即
，①
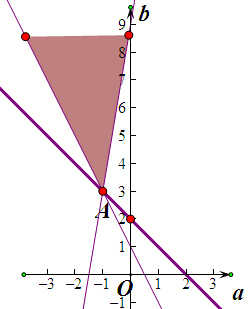
在坐标平面内作直线 1-2a-b=0、9+6a-b=0，它们交于 A（-1，3），满足①（a，b）是 A 点上方区域，
令a+b=t，则 b=-a+t，t是直线在b轴上的截距，
平移直线，可以看出，当直线过A时，t最小为3-1=2．
故a+b的最小值是2．
故选：B．
解：∵f（x）=[x2+（2a-2）x+2-2a-b]ex（a，b∈R）在区间[-1，3]上是减函数，∴f′（x）=ex（x2+2ax-b）＜0，
∴x2+2ax-b＜0，令g（x）=x2+2ax-b，
∵f（x）=[x2+（2a-2）x+2-2a-b]ex（a，b∈R）在区间[-1，3]上是减函数，
∴
|
即
|
在坐标平面内作直线 1-2a-b=0、9+6a-b=0，它们交于 A（-1，3），满足①（a，b）是 A 点上方区域，
令a+b=t，则 b=-a+t，t是直线在b轴上的截距，
平移直线，可以看出，当直线过A时，t最小为3-1=2．
故a+b的最小值是2．
故选：B．
点评：本题主要考查了导数与函数的单调性的问题，以及区域线性规划，属于中档题．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
若双曲线
-
=1的一条渐近线被抛物线y=x2截得的弦长为2
，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
A、
| ||
| B、5 | ||
C、
| ||
D、
|
已知a1，4，a2，1成等差数列，b1，4，b2，1，b3成等比数列，则b2（a2-a1）=（ ）
| A、±6 | B、-6 | C、3 | D、±3 |
已知命题p：?m∈R，m+1≤0，命题q：?x∈R，x2+mx+1＞0恒成立．若p∨q为假命题，则实数m的取值范围是（ ）
| A、m≥2 |
| B、m≤-2 |
| C、m≤-2或m≥2 |
| D、-2≤m≤2 |
已知x＞0，y＞0，2x+3y=1，则4x+8y的最小值为（ ）
| A、8 | ||
| B、6 | ||
C、2
| ||
D、3
|
有一段演绎推理是这样的：“对数函数都是减函数；因为y=lnx是对数函数；所以y=lnx是减函数”，结论显然是错误的，这是因为（ ）
| A、推理形式错误 |
| B、小前提错误 |
| C、大前提错误 |
| D、非以上错误 |
一物体的运动方程为s=sin2t+3t+1，则它的速度方程为（ ）
| A、v=2cos2t+3 |
| B、v=2sin2t+3 |
| C、v=-2cos2t+3 |
| D、v=2cos2t+3t+1 |
已知ab＞0，且
+
≥m恒成立，则m的取值范围是（ ）
| b |
| a |
| a |
| b |
| A、{2} |
| B、[2，+∞） |
| C、（-∞，2] |
| D、[-2，+∞） |