题目内容
已知各项均为正数的数列{an}的前n项和为Sn,且a2n+an=2Sn
(1)求a1
(2)求数列{an}的通项;
(3)若bn=
(n∈N*),Tn=b1+b2+…bn,求证:Tn<
.
(1)求a1
(2)求数列{an}的通项;
(3)若bn=
| 1 |
| an2 |
| 5 |
| 3 |
考点:数列的求和
专题:计算题,等差数列与等比数列
分析:(1)a2n+an=2Sn中令n=1求a1
(2)又a2n+an=2Sn有a2n+1+an+1=2Sn+1,两式相减得并整理得(an+1+an)(an+1-an-1)=0,数列{an}是以a1=1,公差为1的等差数列,以此求数列{an}的通项;
(3)由(2)得出an=n,利用放缩法求证:Tn<
.
(2)又a2n+an=2Sn有a2n+1+an+1=2Sn+1,两式相减得并整理得(an+1+an)(an+1-an-1)=0,数列{an}是以a1=1,公差为1的等差数列,以此求数列{an}的通项;
(3)由(2)得出an=n,利用放缩法求证:Tn<
| 5 |
| 3 |
解答:
解:(1)令n=1,得a12+a1=2S1=2a1,∵a1>0,∴a1=1,
(2)又a2n+an=2Sn,
有a2n+1+an+1=2Sn+1,
两式相减得并整理得(an+1+an)(an+1-an-1)=0,
∵an>0,∴an+1-an=1,∴数列{an}是以a1=1,公差为1的等差数列,
通项公式为an=1+(n-1)×1=n;
(3)n=1时b1=1<
符合…(9分)
n≥2时,因为
<
=
=2(
-
)
所以Tn=b1+b2+…bn<1+2(
-
+
-
+…+
-
)=1+
=
∴Tn<
.
(2)又a2n+an=2Sn,
有a2n+1+an+1=2Sn+1,
两式相减得并整理得(an+1+an)(an+1-an-1)=0,
∵an>0,∴an+1-an=1,∴数列{an}是以a1=1,公差为1的等差数列,
通项公式为an=1+(n-1)×1=n;
(3)n=1时b1=1<
| 5 |
| 3 |
n≥2时,因为
| 1 |
| n2 |
| 1 | ||
n2-
|
| 4 |
| 4n2-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
所以Tn=b1+b2+…bn<1+2(
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 2 |
| 3 |
| 5 |
| 3 |
∴Tn<
| 5 |
| 3 |
点评:本题考查等差数列的判定与通项公式求解,不等式的证明,是数列与不等式的结合.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=CD,AB=4,BC=3,E是PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=CD,AB=4,BC=3,E是PD的中点.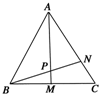 如图所示,在△ABC中,点M是BC的中点,设
如图所示,在△ABC中,点M是BC的中点,设