题目内容

在△ABC中，已知sinA：sinB：sinC=9：6：5，求cosA．
考点：余弦定理
专题：解三角形
分析：由已知设sinA=9k，sinB=6k，sinC=5k，利用正弦定理表示出a，b，c，将三边代入余弦公式计算即可求出值．
解答： 解：设sinA=9k，sinB=6k，sinC=5k，
由正弦定理可得：
a
sinA
=
b
sinB
=
c
sinC
=2R，
可得：a=18kR，b=12kR，c=10kR，
由余弦定理可得：cosA=
b2+c2-a2
2bc
=
(144+100-324)k2R2
240k2R2
=-
1
3
．
点评：此题考查了正弦定理，余弦定理的应用，熟练掌握定理是解本题的关键，属于基本知识的考查．
练习册系列答案
相关题目
已知等差数列{an}的前n项和为Sn（n∈N*），a3=5，S10=100．
（1）求数列{an}的通项公式；
（2）设bn=2 an+2n求数列{bn}的前n项和Tn．
已知
a
=（1，2，-2），
b
=（0，2，4），则
a
，
b
夹角的余弦值为
 
．
已知圆O：x2+y2=1和点A（2，0），若定点B（t，0）（t≠2）和常数λ满足：对圆O上任意一点P，都有|PB|=λ|PA|，则
λ
t
=
 
．
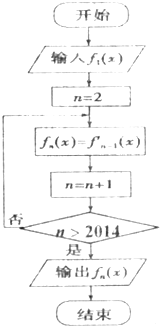在如图所示的程序框图中，当n∈N*（n＞1）时，函数fn（x）等于函数fn-1（x）的导函数，若输入函数f1（x）=sinx+cosx，则输出的函数fn（x）可化为（　　）
A、
2
sin（x+
π
4
）
B、
2
sin（x-
π
4
）
C、-
2
sin（x-
π
4
）
D、-
2
sin（x+
π
4
）
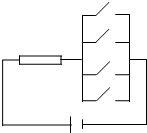某种开关在电路中闭合的概率为p，现将4只这种开关并联在某电路中（如图所示），若该电路为通路的概率为
65
81
，则p=（　　）
A、
1
2
B、
1
3
C、
2
3
D、
3
4
与函数y=x为相同函数的是（　　）
A、y=
x2
B、y=
x2
x
C、y=elnx
D、y=log22x
设a，b∈R，集合M={1，a+b，a}，N={0，
b
a
，b}，若M=N，则b2014-a2013=
 
．
抛掷一个骰子，记A为事件“落地时向上的数为奇数”，B为事件“落地时向上的数是偶数”，C为事件“落地时向上的数是3的倍数”，下面是对立事件的是（　　）
A、A与BB、A与C
C、B与CD、A、B与C

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网