题目内容
已知圆O：x2+y2=1和点A（2，0），若定点B（t，0）（t≠2）和常数λ满足：对圆O上任意一点P，都有|PB|=λ|PA|，则
= ．
| λ |
| t |
考点：两点间的距离公式
专题：计算题,直线与圆
分析：设P（x，y），利用|PB|=λ|PA|，可得（x-t）2+y2=λ2（x-2）2+λ2y2，取（1，0）、（-1，0）分别代入，求得t，λ，即可得出结论．．
解答：
解：设P（x，y），则
∵|PB|=λ|PA|，
∴（x-t）2+y2=λ2（x-2）2+λ2y2，
由题意，取（1，0）、（-1，0）分别代入可得（1-t）2=λ2（1-2）2，（-1-t）2=λ2（-1-2）2，
∴t=
，λ=
，
∴
=
．
故答案为：
．
∵|PB|=λ|PA|，
∴（x-t）2+y2=λ2（x-2）2+λ2y2，
由题意，取（1，0）、（-1，0）分别代入可得（1-t）2=λ2（1-2）2，（-1-t）2=λ2（-1-2）2，
∴t=
| 1 |
| 2 |
| 1 |
| 4 |
∴
| λ |
| t |
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题考查圆的方程，考查赋值法的运用，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
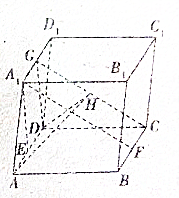如图，四棱柱ABCD=A1B1C1D1的底面是矩形，E，F，G，分别为AD，BC，A1D1的中点，A1E⊥平面ABCD，DH⊥CG，H为垂直（1）求证：A1F∥平面CDG
（2）求证：CG⊥平面ADH．
在△ABC中，已知a=5，b=4，∠C=60°，则C边长为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、5 |