题目内容
已知等差数列{an}的前n项和为Sn(n∈N*),a3=5,S10=100.
(1)求数列{an}的通项公式;
(2)设bn=2 an+2n求数列{bn}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)设bn=2 an+2n求数列{bn}的前n项和Tn.
考点:数列的求和,等差数列的通项公式
专题:等差数列与等比数列
分析:(1)设等差数列{an}的公差为d,由a3=5,S10=100.可得
,解出即可得出;
(2)bn=2 an+2n=22n-1+2n,利用等比数列与等差数列的前n项和公式即可得出.
|
(2)bn=2 an+2n=22n-1+2n,利用等比数列与等差数列的前n项和公式即可得出.
解答:
解:(1)设等差数列{an}的公差为d,∵a3=5,S10=100.
∴
,解得
,
∴an=2n-1.(n∈N*).
(2)bn=2 an+2n=22n-1+2n,
∴数列{bn}的前n项和Tn=
+2×
=
×22n+1-
+n2+n.
∴
|
|
∴an=2n-1.(n∈N*).
(2)bn=2 an+2n=22n-1+2n,
∴数列{bn}的前n项和Tn=
| 2(4n-1) |
| 4-1 |
| n(n+1) |
| 2 |
=
| 1 |
| 3 |
| 2 |
| 3 |
点评:本题考查了等比数列与等差数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
双曲线
-
=1的渐近线方程为( )
| y2 |
| 4 |
| x2 |
| 2 |
A、y=±
| ||||
| B、y=±2x | ||||
C、y=±
| ||||
D、y=±
|
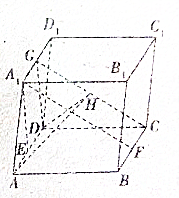 如图,四棱柱ABCD=A1B1C1D1的底面是矩形,E,F,G,分别为AD,BC,A1D1的中点,A1E⊥平面ABCD,DH⊥CG,H为垂直
如图,四棱柱ABCD=A1B1C1D1的底面是矩形,E,F,G,分别为AD,BC,A1D1的中点,A1E⊥平面ABCD,DH⊥CG,H为垂直