题目内容

函数f（x）=lnx+x2-4零点所在的大致区间为（　　）
A、（1，2）
B、（2，3）
C、（3，4）
D、（4，5）
考点：二分法求方程的近似解
专题：函数的性质及应用
分析：函数f（x）=lnx+x2-4在其定义域（0，+∞）上是增函数，f（1）f（2）＜0，由函数零点的判定定理可得函数f（x）=lnx+x2-4零点所在的大致区间．
解答： 解：函数f（x）=lnx+x2-4在其定义域（0，+∞）上是增函数，
再根据f（1）=-3＜0，f（2）=ln2＞0，可得f（1）f（2）＜0，故函数f（x）=lnx+x2-4零点所在的大致区间为（1，2），
故选：A．
点评：本题主要考查用二分法求函数零点的近似值，函数零点的判定定理，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=x-
1
x
（x≠0）
（Ⅰ）判断函数f（x）的奇偶性；
（Ⅱ）求证：函数f（x）在（0，+∞）为单调增函数；
（Ⅲ）求满足f（x）＞0的x的取值范围．
已知两个圆锥有公共底面，且两圆锥的顶点和底面圆周都在半径为3的同一个球面上．若两圆锥的高的比为1：2，则两圆锥的体积之和为
 
．
不等式|x-3|＜m的解集是空集，则m的范围是
 
．
已知函数f（x）=2xlnx+x2-ax+3，其中a∈R．
（Ⅰ）设曲线y=f（x）在点（1，f（1））处的切线与直线2x-y+1=0平行，求a的值；
（Ⅱ）若f（x）≤0在x∈[
1
e
，e]（e=2.718…）上恒成立，求a的取值范围．
在下列区间中，函数f（x）=ex+4x-3的零点所在的区间为（　　）
A、（
1
4
，
1
2
）
B、（-
1
4
，0）
C、（0，
1
4
）
D、（
1
2
，
3
4
）
定义一个新的运算a*b：a*b=
a+b
2
，则同时含有运算符号“*”和“+”且对任意三个实数a，b，c都能成立的一个等式可以是
 
（只要写出一个即可）
已知下列四个命题：
①函数f（x）=2x满足：对任意x1、x2∈R且x1≠x2都有f（
x1+x2
2
）＜
1
2
[f（x1）+f（x2）]；
②函数f（x）=log2（x+
1+x2
），g（x）=1+
2
2x-1
不都是奇函数；
③若函数f（x）满足f（x-1）=-f（x+1），且f（1）=2，则f（7）=-2；
④设x1、x2是关于x的方程|logax|=k（a＞0且a≠1）的两根，则x1x2=1，
其中正确命题的序号是
 
．
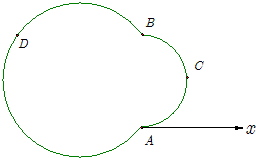在极坐标系中，极点为A，已知“葫芦”型封闭曲线Ω由圆弧ACB和圆弧BDA组成．已知B（4，
π
2
），C（2
2
，
π
4
），D（4
2
，
3π
4
）
（1）求圆弧ACB和圆弧BDA的极坐标方程；
（2）求曲线Ω围成的区域面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网