题目内容
在下列区间中,函数f(x)=ex+4x-3的零点所在的区间为( )
A、(
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(
|
考点:函数零点的判定定理
专题:导数的概念及应用
分析:根据导函数判断函数f(x)=ex+4x-3单调递增,运用零点判定定理,判定区间.
解答:
解:∵函数f(x)=ex+4x-3
∴f′(x)=ex+4
当x>0时,f′(x)=ex+4>0
∴函数f(x)=ex+4x-3在(-∞,+∞)上为f(0)=e0-3=-2<0
f(
)=
-1>0
f(
)=
-2=
-
<0
∵f(
)•f(
)<0,
∴函数f(x)=ex+4x-3的零点所在的区间为(
,
)
故选:A
∴f′(x)=ex+4
当x>0时,f′(x)=ex+4>0
∴函数f(x)=ex+4x-3在(-∞,+∞)上为f(0)=e0-3=-2<0
f(
| 1 |
| 2 |
| e |
f(
| 1 |
| 4 |
| 4 | e |
| 4 | e |
| 4 | 16 |
∵f(
| 1 |
| 2 |
| 1 |
| 4 |
∴函数f(x)=ex+4x-3的零点所在的区间为(
| 1 |
| 2 |
| 1 |
| 4 |
故选:A
点评:本题考察了函数零点的判断方法,借助导数,函数值,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=lnx+x2-4零点所在的大致区间为( )
| A、(1,2) |
| B、(2,3) |
| C、(3,4) |
| D、(4,5) |
函数y=x|x|+px,x∈R是( )
| A、偶函数 |
| B、奇函数 |
| C、即不是奇函数也不是偶函数 |
| D、奇偶性与p有关 |
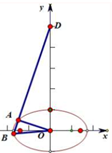 如图,椭圆方程x2+3y2=12,过D(0,10)直线l交椭圆于A、B两点,若OAB为直角三角形,求直线l方程.
如图,椭圆方程x2+3y2=12,过D(0,10)直线l交椭圆于A、B两点,若OAB为直角三角形,求直线l方程.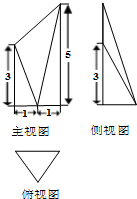 已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为
已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为