题目内容
不等式|x-3|<m的解集是空集,则m的范围是 .
考点:绝对值不等式的解法
专题:不等式
分析:根据绝对值的定义,把不等式左边的|x-3|看作变量,右边的m看作常数,当左边变化时,逐步试取m的值,由左边为非负数可探求右边常数的取值情况.
解答:
解:∵|x-3|≥0,
∴要使不等式|x-3|<m的解集是空集,即关于x的不等式|x-3|<m无实数解,
则m≤0.
故答案为(-∞,0].
∴要使不等式|x-3|<m的解集是空集,即关于x的不等式|x-3|<m无实数解,
则m≤0.
故答案为(-∞,0].
点评:本题属于不等式无解问题,关键是理解不等式中x与m的地位.一般地,若关于x的不等式f(x)<m的解集为空集,则m≤[f(x)]min;若关于x的不等式f(x)>m的解集为空集,则m≥[f(x)]max.值得注意的是,f(x)无最值或原不等式中含等于号时,应细心处理,不可照搬上述结论.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
函数f(x)=lnx+x2-4零点所在的大致区间为( )
| A、(1,2) |
| B、(2,3) |
| C、(3,4) |
| D、(4,5) |
函数y=x|x|+px,x∈R是( )
| A、偶函数 |
| B、奇函数 |
| C、即不是奇函数也不是偶函数 |
| D、奇偶性与p有关 |
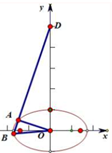 如图,椭圆方程x2+3y2=12,过D(0,10)直线l交椭圆于A、B两点,若OAB为直角三角形,求直线l方程.
如图,椭圆方程x2+3y2=12,过D(0,10)直线l交椭圆于A、B两点,若OAB为直角三角形,求直线l方程.