题目内容
已知函数f(x)=2xlnx+x2-ax+3,其中a∈R.
(Ⅰ)设曲线y=f(x)在点(1,f(1))处的切线与直线2x-y+1=0平行,求a的值;
(Ⅱ)若f(x)≤0在x∈[
,e](e=2.718…)上恒成立,求a的取值范围.
(Ⅰ)设曲线y=f(x)在点(1,f(1))处的切线与直线2x-y+1=0平行,求a的值;
(Ⅱ)若f(x)≤0在x∈[
| 1 |
| e |
考点:利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)先求函数的导函数f'(x),然后求在x=1时的导数值,再与直线2x-y+1=0平行,斜率相等求得a的值,(Ⅱ)先将恒成立问题转化为a≥g(x),然后利用导数求g(x)在x∈[
,e]上的最大值.
| 1 |
| e |
解答:
解:(Ⅰ)f'(x)=2lnx+2+2x-a,
f'(1)=4-a=2⇒a=2.
(Ⅱ)f(x)≤0在x∈[
,e]恒成立?a≥2lnx+x+
在x∈[
,e]恒成立,
令g(x)=2lnx+x+
,则求得g(x)在x∈[
,e]上的最大值即可.
由g′(x)=
知,g(x)在[
,1]上递减,在[1,e]上递增,
故maxg(x)=max{g(
),g(e)}=-2+
+3e.
f'(1)=4-a=2⇒a=2.
(Ⅱ)f(x)≤0在x∈[
| 1 |
| e |
| 3 |
| x |
| 1 |
| e |
令g(x)=2lnx+x+
| 3 |
| x |
| 1 |
| e |
由g′(x)=
| (x-1)(x+3) |
| x2 |
| 1 |
| e |
故maxg(x)=max{g(
| 1 |
| e |
| 1 |
| e |
点评:本题考察导数的基本应用,一是导数的几何意义即切线斜率,二是利用导数判定函数的单调性及求取最值,熟练掌握导数的应用是解决本类题目的关键.

练习册系列答案
相关题目
已知函数f(x)=
,(a>0,a≠1).若数列{an}满足an=f(n)且an+1>an,n∈N*,则实数a的取值范围是( )
|
| A、(7,8) |
| B、[7,8) |
| C、(4,8) |
| D、(1,8) |
函数f(x)=lnx+x2-4零点所在的大致区间为( )
| A、(1,2) |
| B、(2,3) |
| C、(3,4) |
| D、(4,5) |
已知函数f(x)+1=
,当x∈[0,1]时,f(x)=x.若在区间x∈(-1,1]内,g(x)=f(x)-mx-m有两个零点,则实数m的取值范围是( )
| 1 |
| f(x+1) |
A、(0,
| ||
B、[
| ||
C、[0,
| ||
D、[0,
|
如果x∈(-
,0)时总有k(x+
)>cosx成立,则实数k的取值范围是( )
| π |
| 2 |
| π |
| 2 |
| A、(1,+∞) | ||
| B、[1,+∞) | ||
C、(
| ||
D、[
|
设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
| A、若m⊥n,m⊥α,n∥β,则α∥β |
| B、若m∥α,n∥β,α∥β则m∥n |
| C、若m∥n,m∥α,n∥β,则α∥β |
| D、若m⊥α,n∥β,α∥β,则m⊥n |
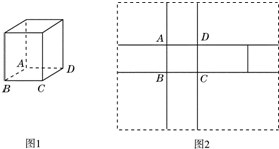 图2中的实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是
图2中的实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是