题目内容
若将函数f（x）=x5表示为f（x）=a0+a1（1+x）+a2（1+x）2+…+a5（1+x）5，其中a0，a1，a2，…，a5为实数，则a3=（ ）
| A、15 | B、5 | C、10 | D、20 |
考点：二项式系数的性质
专题：二项式定理
分析：由题意可得[-1+（x+1）]5=a0+a1（1+x）+a2（1+x）2+…+a5（1+x）5，故有a3=（-1）2•
，计算可得结果．
| C | 3 5 |
解答：
解：由题意可得 f（x）=[-1+（x+1）]5=a0+a1（1+x）+a2（1+x）2+…+a5（1+x）5，
∴a3=（-1）2•
=10，
故选：C．
∴a3=（-1）2•
| C | 3 5 |
故选：C．
点评：本题主要考查二项式定理的应用，二项式展开式的通项公式，求展开式中某项的系数，属于基础题．
练习册系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
（理科）
tan21°tan39°-tan159°+tan39°=（ ）
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
cosα+cosβ=
，sinα+sinβ=
，则cos（α-β ）=（ ）
| 1 |
| 2 |
| 1 |
| 3 |
A、
| ||
B、-
| ||
C、-
| ||
D、-
|
计算2sin15°•cos30°+sin15°等于（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
设物价p（元）与时间t（年）有如下关系：p（t）=（1+5%）t，那么在第10个年头，这种商品的价格上涨速度是（ ）
| A、10（ln1.05）9 |
| B、10ln1.05 |
| C、1.0510ln1.05 |
| D、1.0510 |
已知命题p：?x∈R，2x＜3x；命题q：?x∈R，2x≥1+x2，则命题p，q的真假是（ ）
| A、p真q真 | B、p真q假 |
| C、p假q真 | D、p假q假 |
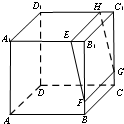如图，平面EFGH为长方体ABCD-A1B1C1D1的截面，E为线段A1B1上异于B1的点，F为线段BB1上异于B1的点，EH∥A1D1，则四边形EFGH的形状是（ ）