题目内容
已知sinα+3cosα=0,求sinα,cosα的值.
考点:同角三角函数间的基本关系,三角函数的化简求值
专题:三角函数的求值
分析:由条件利用同角三角函数的基本关系求得cos α=±
,再根据sin α与cos α异号,可得α在第二、四象限,分类讨论求得sinα,cosα的值.
| ||
| 10 |
解答:
解∵sin α=-3cos α.
又sin2α+cos2α=1,得(-3cos α)2+cos2α=1,即10cos2α=1.∴cos α=±
.
又由sin α=-3cos α,可知sin α与cos α异号,∴α在第二、四象限.
①当α是第二象限角时,sin α=
,cos α=-
.
②当α是第四象限角时,sin α=-
,cos α=
.
又sin2α+cos2α=1,得(-3cos α)2+cos2α=1,即10cos2α=1.∴cos α=±
| ||
| 10 |
又由sin α=-3cos α,可知sin α与cos α异号,∴α在第二、四象限.
①当α是第二象限角时,sin α=
3
| ||
| 10 |
| ||
| 10 |
②当α是第四象限角时,sin α=-
3
| ||
| 10 |
| ||
| 10 |
点评:本题主要考查同角三角函数的基本关系的应用,体现了分类讨论的数学的思想,属于基础题.

练习册系列答案
相关题目
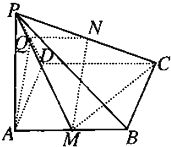 已知PA⊥平面ABCD,四边形ABCD为矩形,PA=AD,M、N分别是AB、PC的中点,求证:
已知PA⊥平面ABCD,四边形ABCD为矩形,PA=AD,M、N分别是AB、PC的中点,求证: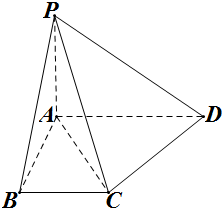 如图,直角梯形ABCD中,∠ABC=∠BAD=90°,
如图,直角梯形ABCD中,∠ABC=∠BAD=90°,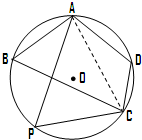 市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4万米,BC=6万米,CD=2万米.
市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4万米,BC=6万米,CD=2万米.