题目内容
cosα+cosβ=
，sinα+sinβ=
，则cos（α-β ）=（ ）
| 1 |
| 2 |
| 1 |
| 3 |
A、
| ||
B、-
| ||
C、-
| ||
D、-
|
考点：两角和与差的余弦函数
专题：三角函数的求值
分析：首先，将给定的两个式子平方相加，然后，借助于两角差的余弦公式求解即可．
解答：
解：∵cosα+cosβ=
，①
sinα+sinβ=
，②
根据①2+②2，得
2+2（cosαcosβ+sinαsinβ）=
，
∴cos（α-β ）=-
，
故选：D．
| 1 |
| 2 |
sinα+sinβ=
| 1 |
| 3 |
根据①2+②2，得
2+2（cosαcosβ+sinαsinβ）=
| 13 |
| 36 |
∴cos（α-β ）=-
| 59 |
| 72 |
故选：D．
点评：本题重点考查了三角公式、两角差的余弦公式等知识，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在等差数列{an}中，a1+a9=10，则a2+a8的值为（ ）
| A、5 | B、6 | C、8 | D、10 |
在数列{an}中，a1=
，an+1=
，则a2013=（ ）
| 4 |
| 5 |
|
A、
| ||
B、
| ||
C、
| ||
D、
|
设i是虚数单位，复数
（a∈R）是纯虚数，则实数a的值是（ ）
| a+3i |
| 1-2i |
| A、-6 | B、-2 | C、6 | D、4 |
设f（x）在（0，+∞）上是单调递增函数，当n∈N*时，f（n）∈N*，且f[f（n）]=2n+1，则（ ）
| A、f（4）=6 |
| B、f（4）=4 |
| C、f（4）=5 |
| D、f（4）=7 |
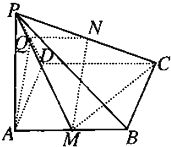已知PA⊥平面ABCD，四边形ABCD为矩形，PA=AD，M、N分别是AB、PC的中点，求证：