题目内容
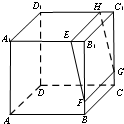如图，平面EFGH为长方体ABCD-A1B1C1D1的截面，E为线段A1B1上异于B1的点，F为线段BB1上异于B1的点，EH∥A1D1，则四边形EFGH的形状是（ ）| A、平行四边形 | B、梯形 |
| C、菱形 | D、矩形 |
考点：棱柱的结构特征
专题：空间位置关系与距离
分析：根据线面平行的判定定理性质定理可得EH∥FG，根据面面平行的性质定理可得EF∥HG，进而可得四边形EFGH是平行四边形，进而由线面垂直的性质定理得到EH⊥EF，得到四边形EFGH为矩形．
解答：
解：∵EH∥A1D1，
∴EH∥BC，
∵EH?侧面BB1C1C，BC?侧面BB1C1C，
∴EH∥侧面BB1C1C，
又∵EH?平面EFGH，平面EFGH∩侧面BB1C1C=FG，
∴EH∥FG，…①
又∵侧面AA1B1B∥侧面CC1D1D，
平面EFGH∩侧面AA1B1B=EF，平面EFGH∩侧面CC1D1D=HG，
∴EF∥HG，…②
由①②得四边形EFGH是平行四边形，
∵EH∥A1D1，
∴EH⊥侧面AA1B1B，
又∵EF?侧面AA1B1B，
∴EH⊥EF，
四边形EFGH为矩形，
故选：D
∴EH∥BC，
∵EH?侧面BB1C1C，BC?侧面BB1C1C，
∴EH∥侧面BB1C1C，
又∵EH?平面EFGH，平面EFGH∩侧面BB1C1C=FG，
∴EH∥FG，…①
又∵侧面AA1B1B∥侧面CC1D1D，
平面EFGH∩侧面AA1B1B=EF，平面EFGH∩侧面CC1D1D=HG，
∴EF∥HG，…②
由①②得四边形EFGH是平行四边形，
∵EH∥A1D1，
∴EH⊥侧面AA1B1B，
又∵EF?侧面AA1B1B，
∴EH⊥EF，
四边形EFGH为矩形，
故选：D
点评：本题考查的知识点是棱柱的结构特征，线面平行和线面垂直的性质和判定，难度不大，属于基础题．
练习册系列答案
相关题目
设f（x）在（0，+∞）上是单调递增函数，当n∈N*时，f（n）∈N*，且f[f（n）]=2n+1，则（ ）
| A、f（4）=6 |
| B、f（4）=4 |
| C、f（4）=5 |
| D、f（4）=7 |
等差数列{an}的前n项和为Sn，且S2=6，a1=4，则公差d等于（ ）
| A、3 | B、2 | C、1 | D、-2 |
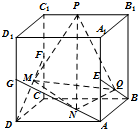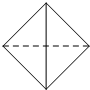
已知点E、F、G分别是正方体ABCD-A1B1C1D1的棱AA1、CC1、DD1的中点，点M、N、Q、P分别在线段DF、AG、BE、C1B1上．以M、N、Q、P为顶点的三棱锥P-MNQ的俯视图不可能是（ ）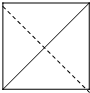
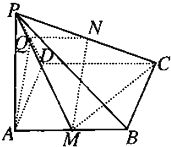已知PA⊥平面ABCD，四边形ABCD为矩形，PA=AD，M、N分别是AB、PC的中点，求证：
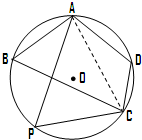市某棚户区改造建筑用地平面示意图如图所示．经规划调研确定，棚改规划建筑用地区域是半径为R的圆面．该圆面的内接四边形ABCD是原棚户建筑用地，测量可知边界AB=AD=4万米，BC=6万米，CD=2万米．